Analyse d'une oeuvre d'art

Le Nombre d’Or et la Peinture

Nous avons vu plus haut que les proportions humaines étaient à l’origine d’un système de mesures utilisé depuis l’antiquité. Le rapport entre ces mesures a été nommé le nombre d’Or, dont nous retrouvons la trace dans des domaines aussi variés que les mathématiques, la géométrie, l’architecture ou la typographie.

C’est aussi le cas dans le domaine de la peinture; à partir du moment ou les peintres ont su maîtriser la perspective, et ou la représentation picturale devenait plus réaliste, les peintres ont structuré leurs oeuvres à l’aide du système de mesures de leur époque.

Au moyen-âge, la peinture était avant tout signifiante, c’est à dire symbolique. La taille des personnages était fonction de leur importance et de leur dignité. L’image ci-contre est un exemple de perspective inversée, ou les personnages les moins importants sont plus petits que les sujets principaux, même s’ils sont placés au premier plan.

A partir de la Renaissance, une perspective plus réaliste s’invite dans les tableaux des maîtres de l’époque. La représentation de l’Annonciation par Fra Angelico (1400 - 1455) montre que les principes de la perspective ont été acquis, et que les personnages ont une taille réaliste par rapport aux bâtiments.

Dans les décennies qui suivent, les peintres utilisent le système de mesure en vigueur pour structurer leurs oeuvres: les personnages sont placés à des endroits précis, que l’on appelle aujourd’hui des centres d’intérêt ou des points de focale.

Paul Véronèse peint les Noces de Cana vers 1562. La perspective est parfaitement maitrisée. Les groupes de personnages se répartissent de façon réfléchie, et nous assistons à une véritable mise en scène cinématographique, cadrée sur des principes géométriques très stricts; la grille superposée au tableau de Véronèse ci-dessous, permet d’imaginer cette mise mise en scène basée sur la géométrie.

La maîtrise générale de ces effets de représentation permet aussi au peintre de « voir en grand ». La taille des oeuvres de cette époque n’a plus rien à voir avec celle des enluminures du moyen-âge : le tableau mesure presque 7 mètres sur 10 !

Analyse de la structure d’un tableau de la Renaissance italienne

Nous en savons maintenant assez concernant le système de mesures qui a précédé le système métrique décimal pour analyser la façon dont a été structuré un des plus célèbre des tableaux de la renaissance italienne, la «naissance de Vénus», peint par Sandro Botticelli vers 1485.

La Naissance de Vénus

Vénus naît d’un coquillage. Sur sa gauche, nous découvrons Zéphyr et Chloris. Zéphyr est le fils d’Eole, dieu des vents, et Chloris, sa femme, est une nymphe qui règne sur l’empire des fleurs. Ils soufflent sur Vénus comme pour la déshabiller ou la sécher de l’eau qui l’a vu naître, mais aussi pour la purifier et la couvrir de fleurs. A la droite de Vénus se trouve une « heure », fille de Zeus, une des maîtresses du temps. Elle semble vouloir recouvrir Vénus d’un tissu orné de fleurs pour cacher sa nudité, ou la réchauffer.

Botticelli s’est inspiré, pour représenter Vénus, de Simonetta Cattaneo, une des plus belles femmes de Florence, épouse du riche marchand Marco Vespucci et peut-être maîtresse de Giuliano de Medici, dont le frère Lorenzo régnait alors sur la ville. Simonetta mourut très jeune, et le peintre la prit comme modèle posthume dans nombre de ses tableaux. Amoureux platonique de la belle, Botticelli voulu, à son décès, être enterré auprès d’elle. Leurs deux corps reposent aujourd’hui à Florence, dans l’église Ognissanti.

Analyse du positionnement des personnages du tableau

Observez comment ces personnages sont placés dans le tableau. Observez aussi la ligne d’horizon, limite entre la mer et le ciel. Elle ne se situe pas au milieu de la hauteur du tableau, de même que Vénus, le personnage central de l’oeuvre, n’est pas situé exactement au centre du tableau.

Le tableau mesure 2.78 mètres de largeur sur 1.72 mètres de hauteur. Ces mensurations paraissent abstraites, mais rappelons-nous qu’à l’époque, on mesurait en pieds et en coudées.

Nous savons aujourd’hui que la coudée mesurait entre 53 et 55 cm et le pied entre 33 à 36 cm. Nous savons aussi que les peintres avaient l’habitude de diviser la hauteur de leur toile en huit afin de la quadriller et de placer ensuite les éléments principaux de leurs tableaux.

Si nous divisons la hauteur de ce tableau par 8, nous obtenons 21.5 cm. Et si nous divisons sa largeur par 8, nous trouvons 34.7 cm.

21.5 cm semble être la mesure de l’empan et 34.7 cm celui du pied, mesures utilisées à l’époque. Peut-être étaient-ce les propres mesures de Sandro Botticelli ?

Le tableau devait donc mesurer à l’époque 5 x 3 coudées , ou 8 x 5 pieds, ou 13 x 8 empans !

Quadrillage du tableau en mesures de l’époque

Commençons à quadriller le tableau avec une grille régulière formés de carrés mesurant, à l’échelle du tableau, 35 cm de côté, soit la longueur de la mesure du pied. Nous nous apercevons que les différents personnages du tableau se répartissent comme suit:

Zéphyr et Chloris occupent un rectangle de 3 carrés de largeur sur 5 de hauteur sur la gauche du tableau, et l’Heure, fille de Zeus, le même rectangle sur sa droite.

Vénus, quant à elle, s’inscrit dans un rectangle au milieu du tableau, de 2 carrés de largeur sur 5 de hauteur. La ligne d’horizon a l’air de coïncider avec une des lignes du quadrillage, et la coquille qui donne naissance à Vénus s’inscrit pratiquement dans un rectangle de 3 carrés de largeur sur 2 de hauteur.

Vous vous rappelez que nous avons divisé plus haut la largeur du tableau par 8; quadrillons-le maintenant avec une grille régulière formés de carrés de 21.5 cm de côté, en divisant sa hauteur par 8.

21,5 cm est la longueur approximative de l'empan.

Zéphyr et Chloris occupent un rectangle de 5 carrés de largeur sur 8 de hauteur sur la gauche du tableau, et l’Heure, fille de Zeus, le même rectangle sur sa droite.

Vénus s’inscrit dans un rectangle au milieu du tableau, de 3 carrés de largeur sur 8 de hauteur. Qui plus est, elle parait être centrée sur une des lignes de ce nouveau quadrillage. La ligne d’horizon coïncide avec une des lignes de ce quadrillage, et la coquille est contenue dans un rectangle de 6 carrés de largeur sur 3 de hauteur.

Nous observons que le découpage du tableau (Ligne d’horizon, emplacement des différents personnages) est quasiment identique, que l’on quadrille le tableau en 5x8 ou en 8X13 carrés. Le découpage en 8x13 parait juste plus « affiné ».

Observons aussi que 3, 5, 8 et 13 font partie des premiers chiffres de la célèbre suite du mathématicien Fibonacci, et que diviser 8 par 5, et 13 par 8 donne une valeur de plus en plus approchante de 1.618 !!!

Un tracé régulateur basé sur le nombre d’Or

Si nous devions, avec nos moyens d’aujourd’hui (calculettes, ordinateurs) dessiner un tracé régulateur basé sur le nombre d’Or, nous procéderions ainsi: prenons un rectangle de même format que celui du tableau de Botticelli, et divisons sa largeur par 1.618: nous obtenons la figure ci-dessous. La largeur totale du rectangle divisée par 1.618 permet de tracer une verticale qui partage le rectangle en un carré à gauche, et un rectangle à droite. Continuons à diviser le petit rectangle de la même façon deux fois de suite.

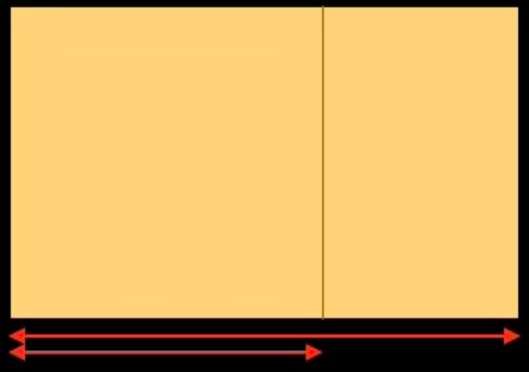
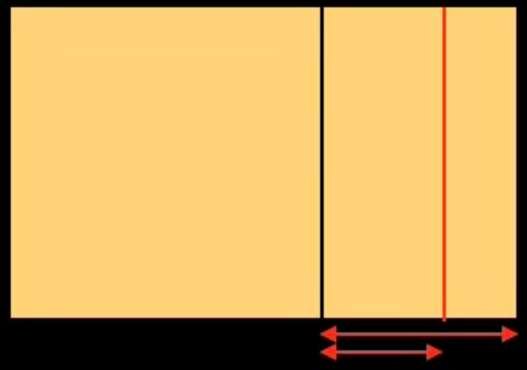
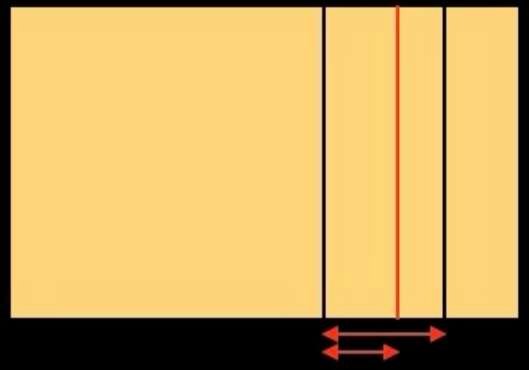
Nous avons obtenu trois subdivisions dans la partie droite du rectangle initial. Effectuons la même opération dans la partie gauche: nous obtenons la figure ci-dessous à gauche. Nous avons divisé le rectangle initial verticalement 6 fois. Nous allons maintenant le diviser horizontalement. Nous obtenons la figure ci-dessous à droite.

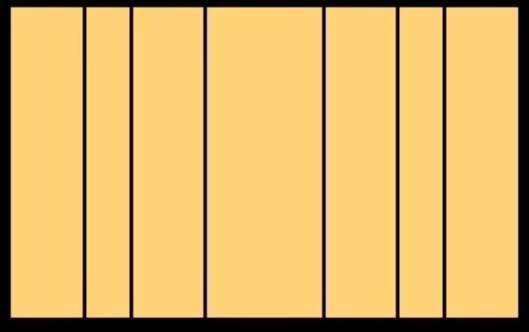
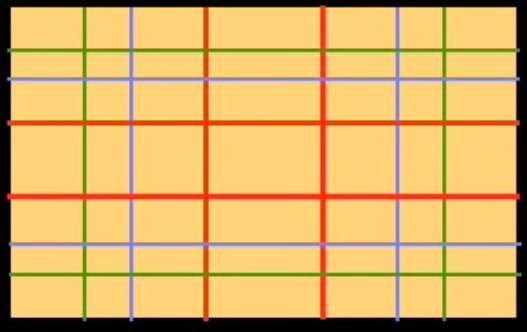
Rajoutons quelques couleurs à ce dernier découpage pour y voir plus clair: Les lignes rouges représentent la première division de la largeur et de la hauteur du rectangle initial par le nombre d’Or. Nous l’appellerons la division primaire.

Les lignes bleues représentent une division secondaire (c’est la division des rectangles créés par la première division), et les lignes vertes une division tertiaire, c’est à dire la division des rectangles créés par la deuxième division.

Nous allons maintenant superposer ce « tracé régulateur » moderne sur le tableau de Botticelli, et le comparer aux tracés obtenus par les deux quadrillages 5x8 et 8x13 précédents.

Quadrillage 5x8

(Mesure en pieds)

Quadrillage 8x13

(Mesure en empans)

Tracé régulateur obtenu par le Golden Divider for Arts

Nous nous apercevons que le découpage interne du tableau est pratiquement identique: la ligne d’horizon est à peu de choses près à la même place, et les personnages et groupes de personnages du tableau occupent les mêmes surfaces.

Que peut-on en déduire ?

Nous savons que Botticelli ne possédait à l’époque ni calculette, ni « mètre ruban ». Il ne pouvait donc placer les centres d’intérêt de son tableau qu’à l’aide de ses propres mensurations.

Botticelli avait appris son art d’un moine peintre nommé Fra Filippo Lippi, qui lui avait certainement enseigné la façon de structurer un tableau d’une façon symbolique, c’est à dire en utilisant des mesures et des proportions humaines, donc divines. Ce savoir faire était un secret de fabrication, tout comme celui des maîtres d’oeuvre de la construction, et se transmettait de maître à élève, de génération en génération.

Concernant le tracé régulateur ordonnant le tableau de Botticelli, il n’est pas du tout certain que le peintre connaissait la suite de Fibonacci, ou même qu’il connaissait le nombre d’Or. Nous n’imaginons pas Sandro Botticelli prendre une calculatrice - qui n’existait pas à l’époque - et diviser la hauteur et la largeur de son tableau par (1+√5)/2 !

Mais nous savons aujourd’hui qu’en divisant la hauteur de sa toile par 8, et en utilisant les mesures de son époque, le résultat obtenu était pratiquement le même. Ce secret de fabrication, certainement d’inspiration religieuse, était donc accessible par une simple géométrie: une ficelle suffit à pouvoir diviser une longueur en 2, puis en 4 et en 8. De la même façon, l’utilisateur d’une corde à 13 noeuds pour vérifier un angle droit ne se doute pas un instant de la portée historique, géométrique et quasi-mystique de l’outil qu’il manipule.

La notion de nombre d’Or était inhérente au système de mesures utilisé pas nos ancêtres: ils l’utilisaient sans devoir le connaître. En effet, la combinaison de mesures utilisées telles que la coudée, le pied et l’empan faisait apparaître « mathématiquement » les proportions « dorées ».

Nous retrouvons de façon inconsciente dans le tableau de Botticelli des proportions humaines et familières, et c’est sans doute pour cette raison que cette oeuvre nous paraît équilibrée.

Comparez le placement de la ligne d’horizon par rapport à la hauteur du tableau et à la position de l’articulation du poignet dans un avant bras humain. Les différents groupes composant le tableau sont disposés également selon cette même logique.

D’après le système de mesures des bâtisseurs de cathédrales, si la longueur de la coudée est la distance du coude au bout de la main tendue, la longue du pied serait donc celle de l’avant bras sans la longueur de la main, et la longueur de la main serait équivalente à celle de l’empan, c’est à dire la largeur de la main les doigts écartés.

Analyse de la structure de tableaux d’époques différentes

Diego Velasquez - Venus au miroir - 1647

Observez la disposition du corps de Vénus, qui s’inscrit dans un rectangle allongé occupant les deux tiers du bas du tableau (en pointillés ci.dessus). Son buste s’inscrit dans un rectangle, marqué ici en rouge, en bas à droite du tableau. Un rectangle identique cadre le chérubin, en haut à gauche, en symétrie diagonale.

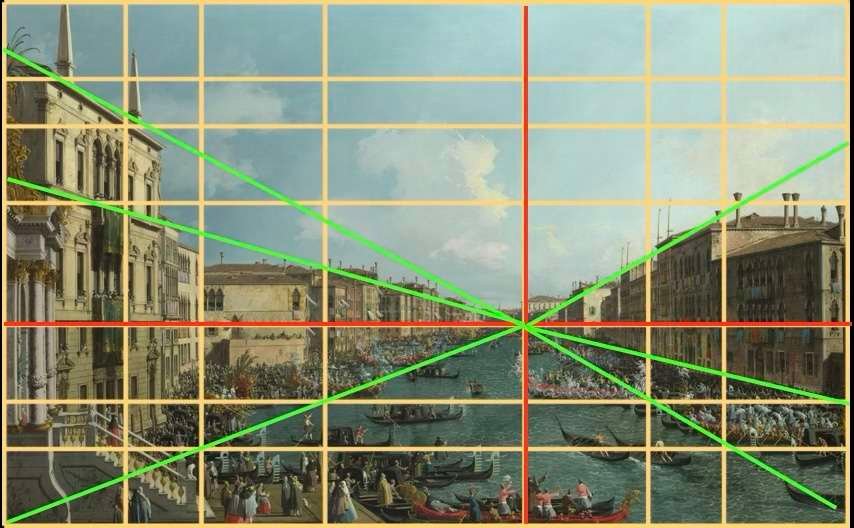
Canaletto - Régate sur le Grand Canal - 1740

Observez ici la placement de la ligne d’horizon, et le point de fuite du tableau situé sur celle-ci, à l’intersection des deux lignes rouges. Toutes les lignes de fuite, en vert, convergent vers ce point de fuite unique.

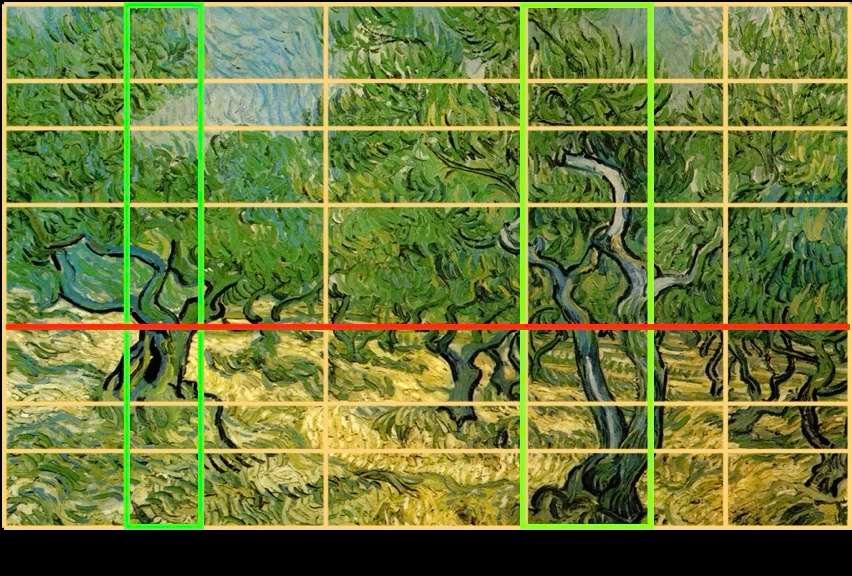
Vincent Van Gogh - Les oliviers - vers 1889

La ligne d’horizon, ici en rouge, délimite le sol du feuillage des oliviers. Les deux troncs d’arbres principaux, en vert, sont au centre de deux rectangles délimités par les flèches sous le tableau. Si chaque arbre est symétrique en soi, la dissymétrie des deux arbres donne au tableau une dynamique harmonieuse.

Ferdinand Hodler - Le delta du Maggia avant le lever du soleil - 1893

Le « découpage » du tableau devient ici évident grâce à la grille de structure: le rectangle allongé du haut délimite la chaine de montagnes, celui du milieu la glace et celui du bas l’eau claire. La ligne d’horizon, en rouge, est délimitée par les deux rectangles hauts.

Ci-dessous, deux tableaux de maîtres dont les proportions extérieures sont différentes de celles du rectangle d’or. La structure interne de ces tableaux fait penser pourtant que le nombre d’or a été, consciemment ou non, utilisé.

Leonard de Vinci- l’Annonciation - 1472

Ce tableau n’est pas au format d’un rectangle d’or, mais le découpage interne de sa structure, en rouge, établi selon la règle d’or, fait apparaître quatre rectangles dont les lignes délimitent la ligne d’horizon, l’angle du bâtiment et le positionnement respectif des personnages.

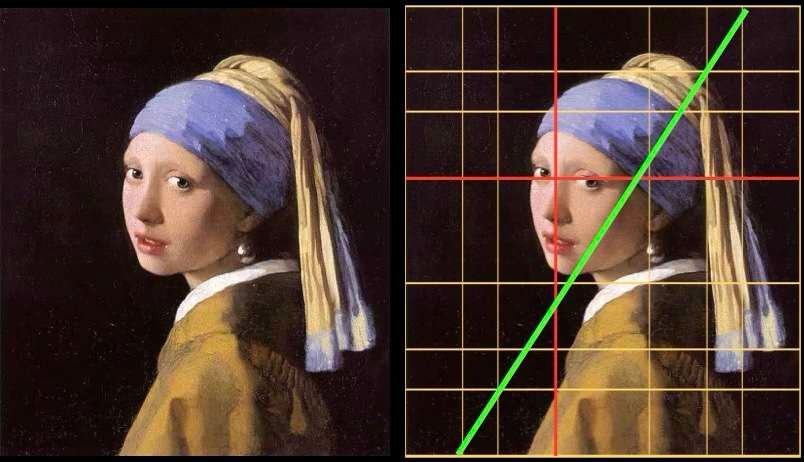
Johannes Vermeer - La jeune fille à la perle - 1665

Un premier examen rapide nous fait penser que le visage de la jeune fille est au centre du tableau. Mais si on superpose une grille de structure basée sur le nombre d’Or, on s’aperçoit du positionnement spécifique du visage de la jeune fille: les lignes rouges déterminent avec précision l’alignement de ses yeux et l’axe vertical de son visage. Une ligne diagonale, en vert sur l’image, délimite l’ombre et la lumière.

Nombre d’Or et design industriel

Il existe sans aucun doute un rapport entre l’esthétique et la fonctionnalité: en d’autres termes, ce qui est beau est fonctionnel, et tout ce qui est fonctionnel est beau, tout comme dans le corps humain. Les différentes exemples ci-dessous illustrent la façon dont le nombre d’Or nous signale sa présence quotidiennement.
Bien des objets présents dans notre vie courante ont des proportions qui se rapprochent des proportions d’un rectangle d’Or, et donc du corps humain.

Le format de certains livres, d’une radio, d’une boite de parfum ou le rapport entre les dimensions d’une fenêtre en sont des exemples frappants. Vous remarquerez que beaucoup de fenêtres ont les proportions du rectangle d’Or, et il n’y a rien d’étonnant à cela; l’habitude avait été prise de donner aux fenêtres courantes les dimensions suivantes : trois pieds de large sur trois coudées de hauteur, soient les proportions parfaites d’un rectangle d’Or !

Ci-dessous, un tracé régulateur a été superposé sur des silhouettes de bateau, d’avion, de voiture ou même d’arme de poing. La dissymétrie apparente des volumes est appelée symétrie dynamique.

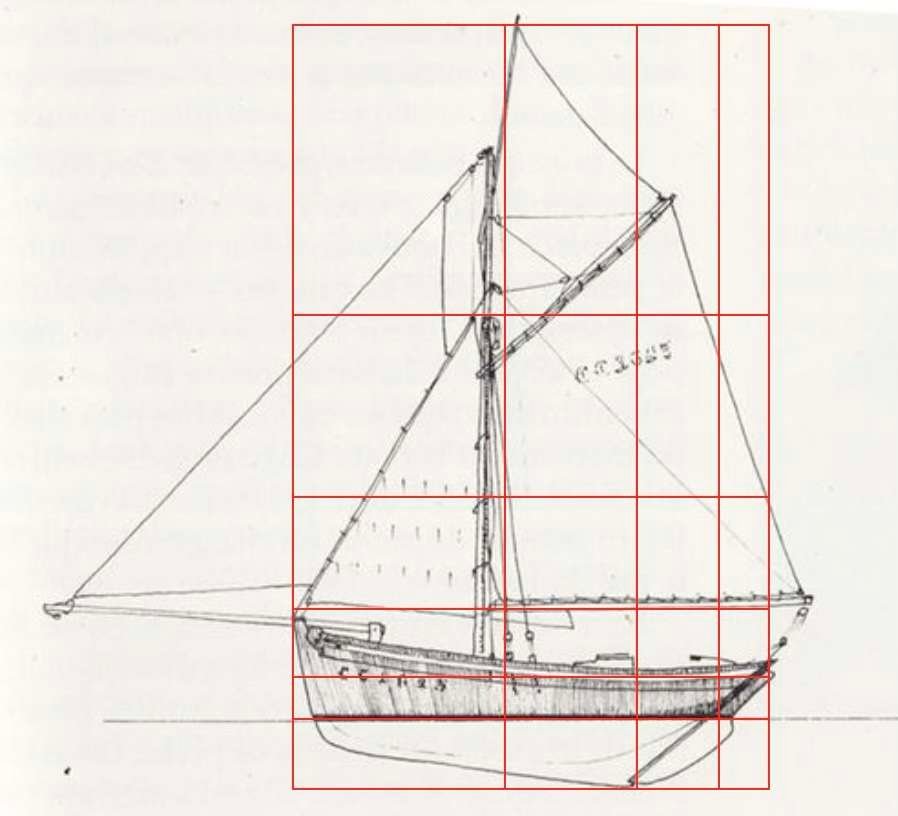
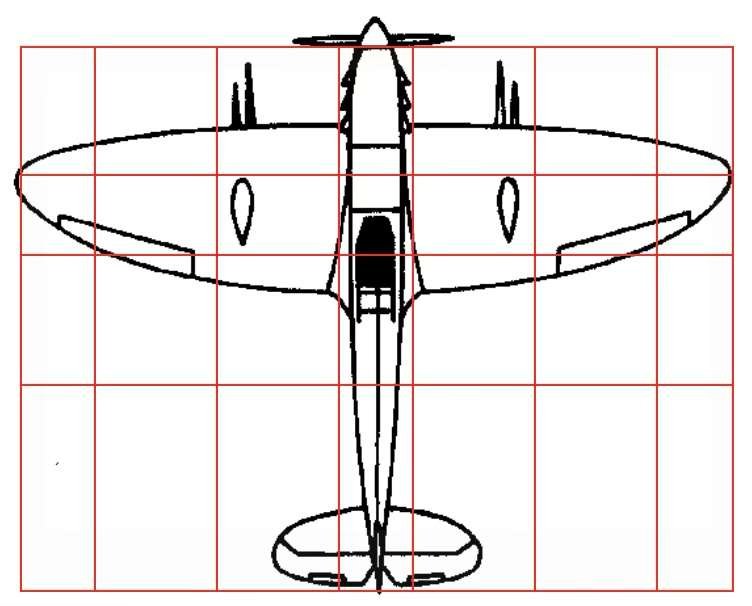
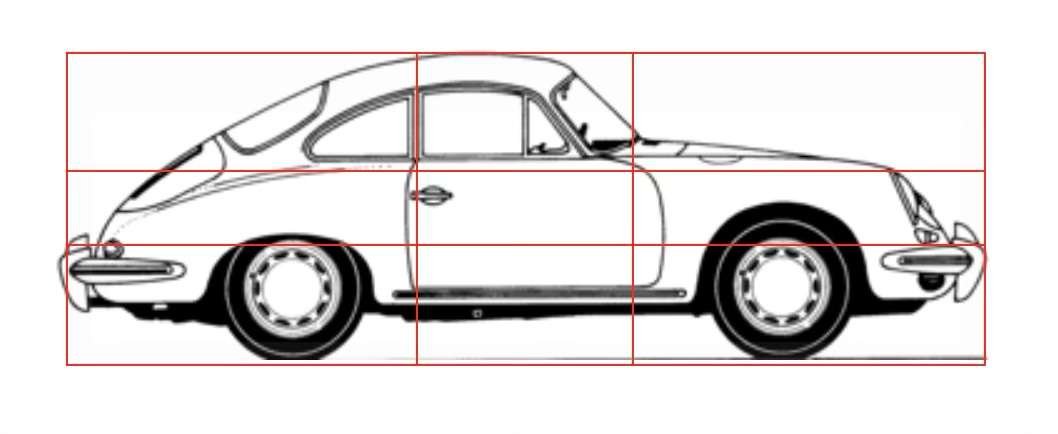
Les proportions utilisées dans la construction marine, aéronautique, automobile ou militaire montrent que l’esthétique et la fonctionnalité ont un rapport indissociable.

Le Nombre d’Or et l’architecture

Le Nombre d’or a inspiré l’architecture des périodes antiques, médiévales et de la Renaissance, grâce, nous l’avons-nous vu, à un système de mesures basé sur ce concept.

La pyramide de Kheops, le Parthenon d’Athènes, la cathédrale de Notre Dame à Paris, ainsi que la plupart des bâtiments sacrés construits en Europe au moyen-âge, la grande mosquée de Kairouan en Tunisie, le Taj Mahal en Inde en sont des exemples reconnus.

Mais le Nombre d’Or est-il encore utilisé aujourd’hui dans cette discipline ?

Après la deuxième guerre mondiale, l’architecte franco-suisse Charles-Édouard Jeanneret-Gris, dit Le Corbusier (1887 - 1965), reprit les théories de l’architecte romain Vitruve, en voulant adapter l’urbanisme, l’architecture et même le mobilier à la morphologie humaine.

Il mit au point en 1945 une notion architecturale, le Modulor, qui permettait de standardiser l’environnement humain en fonction de ses propres proportions.

Le nom «Modulor» est, en français, une contraction de «module» et de «nombre d’or».

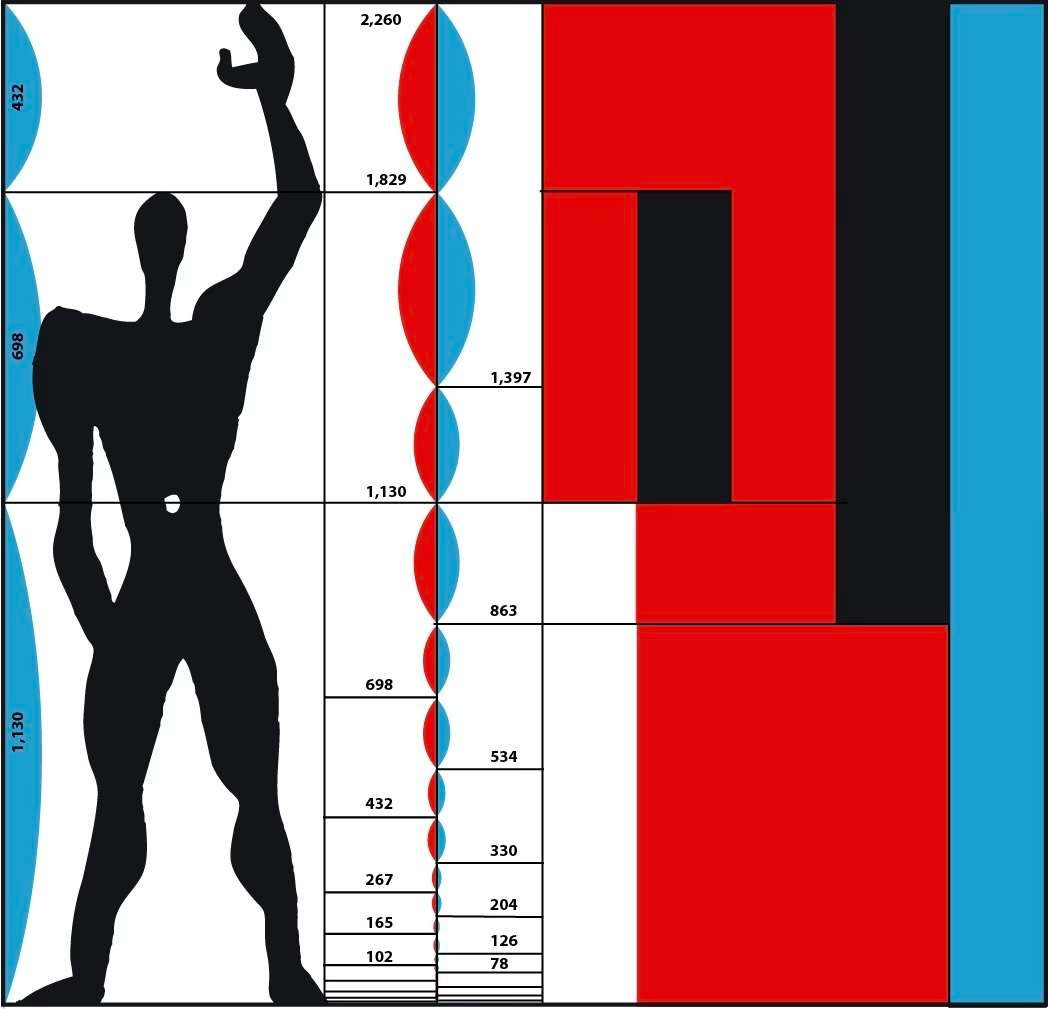
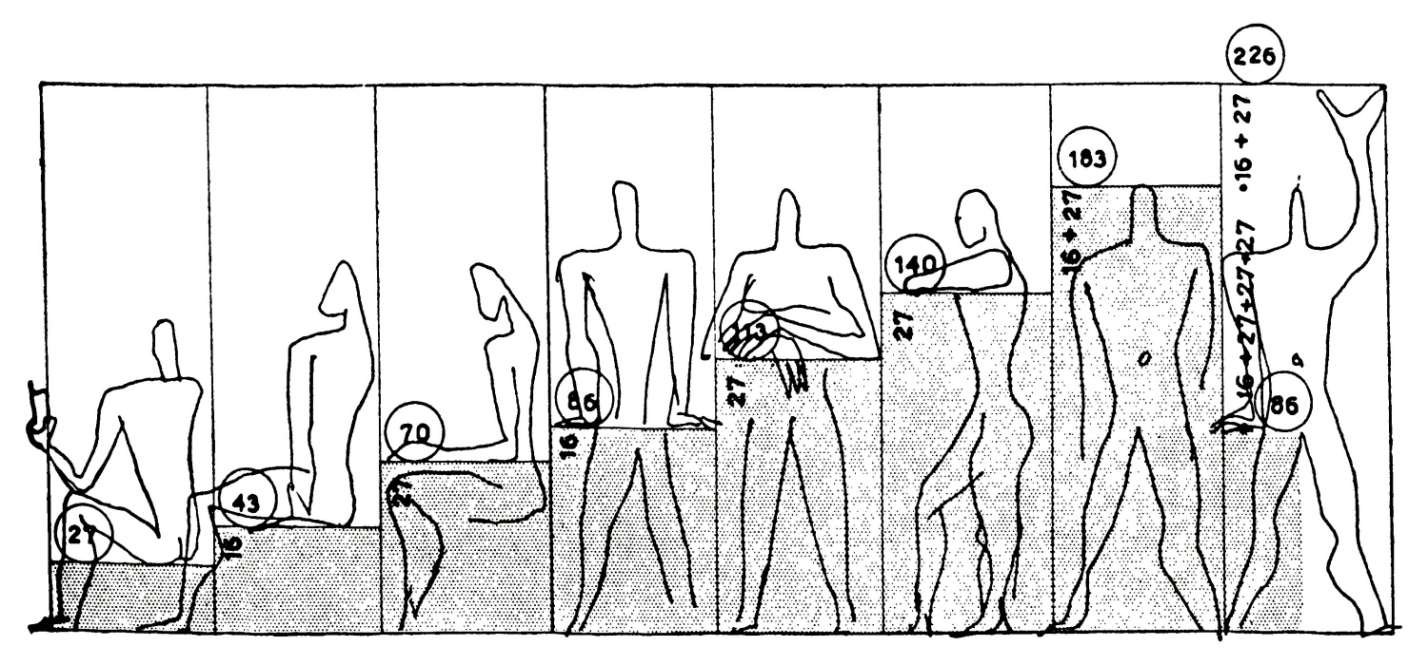
Si les projets réalisés par Le Corbusier sont relativement peu nombreux, les plus connus parmi les dix-sept sites étant le musée national des arts occidentaux de Tokyo (1959), Le musée national des arts occidentaux de Tokyo (1959), la ville de Chandigarh en Inde (1951), La villa Savoye (1928-1931), la Cité Radieuse de Marseille (1952) et la chapelle de Notre-Dame-du-Haut à Ronchamp (1953-1955), il influença néanmoins toute une génération d’architectes dans le monde entier.

L’idée de concevoir un habitat et une architecture d’intérieur compatibles avec les proportions humaines séduit encore aujourd’hui un grand nombre d’architectes de toutes nationalités.

Avons-nous trouvé le rectangle d’Or ?

Oui, car nous en sommes littéralement entourés, si nous regardons bien autour de nous ! Bien sûr, nous ne mesurons plus ce qui nous entoure en pieds et en coudées, et le système métrique décimal a certainement, de par son côté abstrait et tellement différent du corps humain, brouillé les pistes dans notre façon de percevoir et d’évaluer notre environnement.

Mais les habitudes prises au fil des siècles sont restées; l’évaluation d’une silhouette humaine, d’une oeuvre architecturale, d’un tableau ou même d’un objet passe encore et toujours aujourd’hui par une comparaison inconsciente avec les proportions humaines.

Le nombre d’Or, ce rapport si spécial entre la hauteur et la largeur d’un rectangle d’Or, se retrouve inconsciemment dans une main ou un visage, lesquels, à peu de choses près, s’inscrivent dans cette figure géométrique.

L’idée que nous nous faisons de l’harmonie et de la beauté est indissociable de la perception que nous avons du corps humain. C’est sans doute cette analyse inconsciente que nous faisons constamment qui provoque chez nous l’intérêt et l’attirance ou au contraire l’indifférence ou l’aversion lorsque nous contemplons une oeuvre faite par l’homme.

Si vous désirez approfondir vos connaissances sur le nombre d’Or, vous découvrirez vite que certains auteurs en font une règle absolue et universelle, et que d’autres, au contraire, crient à la supercherie mystique. Ce sera à vous de vous en faire une idée plus précise.

Ce qui est certain, c’est que le nombre d’Or est une réalité mathématique et géométrique (les élèves du collège, qui doivent résoudre des équations du type x2 - x - 1 = 0 ne diront pas le contraire !).

Sa présence dans la structure du corps humain peut être éventuellement discutée dans son exactitude, mais les proportions humaines ont bien donné naissance à un système de mesures organisé et géométriquement parfait.

Depuis l’apparition du système métrique décimal, qui n’a plus de rapport avec le corps humain, notre vision du rapport entre l’harmonie qui se dégage d’un objet, d’une oeuvre architecturale ou d’une oeuvre d’art et l’harmonie des proportions du corps humain s’en est trouvée brouillée. Mais les réflexes accumulés depuis des siècles ont la vie dure !