Em busca do retângulo de ouro
Em geometria, um retângulo áureo é um retângulo cuja razão entre a largura e a altura é igual a um número chamado razão áurea, cujo valor aproximado é 1,618. A letra grega 𝚽 (pronuncia-se "Phi") simboliza este número.

Este retângulo simboliza a harmonia perfeita entre dois comprimentos desiguais: a sua largura e a sua altura.
Esta relação muito especial entre dois comprimentos pode ser observada no corpo humano, nomeadamente quando se compara o tamanho das falanges dos dedos, mas também da mão e do antebraço, ou a posição do umbigo em relação à altura do corpo.
Para procurar o retângulo de ouro, vamos recuar no tempo para saber como as pessoas mediram e construíram o seu ambiente desde a Antiguidade.
Vamos ao Egito antigo, a terra dos faraós, conhecer os construtores de catedrais da Idade Média, matemáticos e cientistas como Leonardo Fibonacci, Luca Pacioli e Leonardo da Vinci, arquitectos e os grandes mestres da pintura do Renascimento italiano, como Andrea Palladio e Sandro Botticelli, filósofos do século XIX e início do século XX e, finalmente, o famoso arquiteto franco-suíço Le Corbusier, que quis conciliar o sistema de medidas utilizado pela humanidade durante séculos com o sistema métrico, que nasceu "apenas" após a Revolução Francesa de 1789.
Através de todas estas descobertas, vamos analisar a estrutura de vários quadros de pintores antigos famosos, como Botticelli, Velasquez e Canaletto, bem como de artistas mais contemporâneos, como Van Gogh e Ferdinand Hodler, e perceber porque é que as suas obras parecem tão harmoniosas.
Depois de estudar estas pinturas, tentaremos responder a uma pergunta difícil: por que razão consideramos uma obra (arquitetónica ou pictórica) ou um objeto (artesanal ou industrial) agradável à vista?
Porque é que consideramos harmoniosa uma criação humana?
Veremos então que as proporções deste retângulo particular estão muito presentes no nosso ambiente.
Quando terminar de ler esta brochura, terá aprendido a reconhecê-lo, conhecerá a sua história e reconhecê-lo-á (quase) em todo o lado!
O Egito dos faraós
Atualmente, medimos os comprimentos em metros e centímetros, mas este sistema de medida, o sistema métrico decimal, surgiu muito recentemente na história da humanidade.
No antigo Egito, a medida padrão era o côvado. O côvado é a distância entre a ponta do cotovelo e a extremidade da mão estendida.
Atualmente, chamamos-lhe o côvado real ou o côvado grande. Atualmente, mede entre 52 e 54 centímetros. Os arquitectos egípcios utilizavam esta medida como referência para a construção de edifícios e monumentos.

Conquista após conquista, o território do império egípcio tornou-se muito vasto; os faraós decidiram impor uma única medida, o côvado, para facilitar as transacções comerciais.
Mandaram fazer milhares de réguas graduadas e distribuíram-nas por todo o império para que todos pudessem utilizar a mesma unidade de medida. A medida padrão do côvado era o côvado do próprio Faraó. A régua era subdividida em submedidas do côvado.
Os construtores egípcios utilizavam uma corda com treze nós (doze intervalos) para traçar as plantas dos seus monumentos e também para calcular os ângulos. Cada intervalo entre dois nós equivalia a um côvado. A corda com nós podia ser utilizada para desenhar muitas formas geométricas diferentes, incluindo um ângulo reto, como mostra a figura vermelha ao lado.
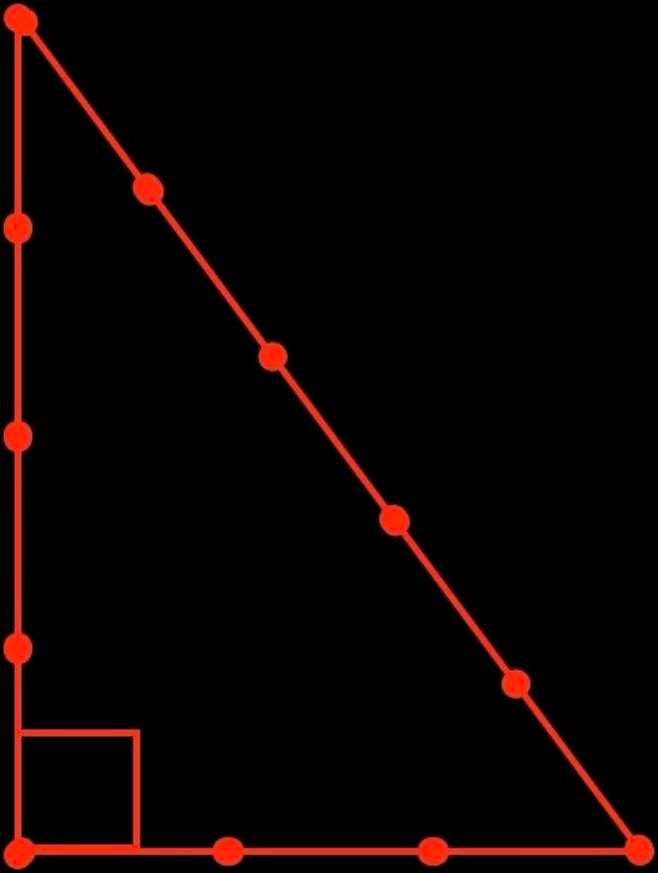
Este triângulo é conhecido como triângulo "3,4,5" ou triângulo egípcio. Ainda hoje é utilizado por alguns profissionais da construção civil para garantir que um canto é quadrado.
O Império Romano também utilizava o côvado como unidade de medida, assim como o pé, a palma da mão e o dedo. Ao longo dos séculos e entre diferentes países, a medida do côvado tem variado. Na época romana, representava um comprimento de cerca de 45 cm.
O homem vitruviano
Marcus Vitruvius Pollio, conhecido como Vitruvius, foi um arquiteto romano que viveu no século I a.C. (pensa-se que o seu nascimento terá ocorrido por volta de 80 a.C. e a sua morte por volta de 15 a.C.1).
É do seu tratado, De architectura, que provém a maior parte do nosso conhecimento das técnicas de construção na antiguidade clássica.
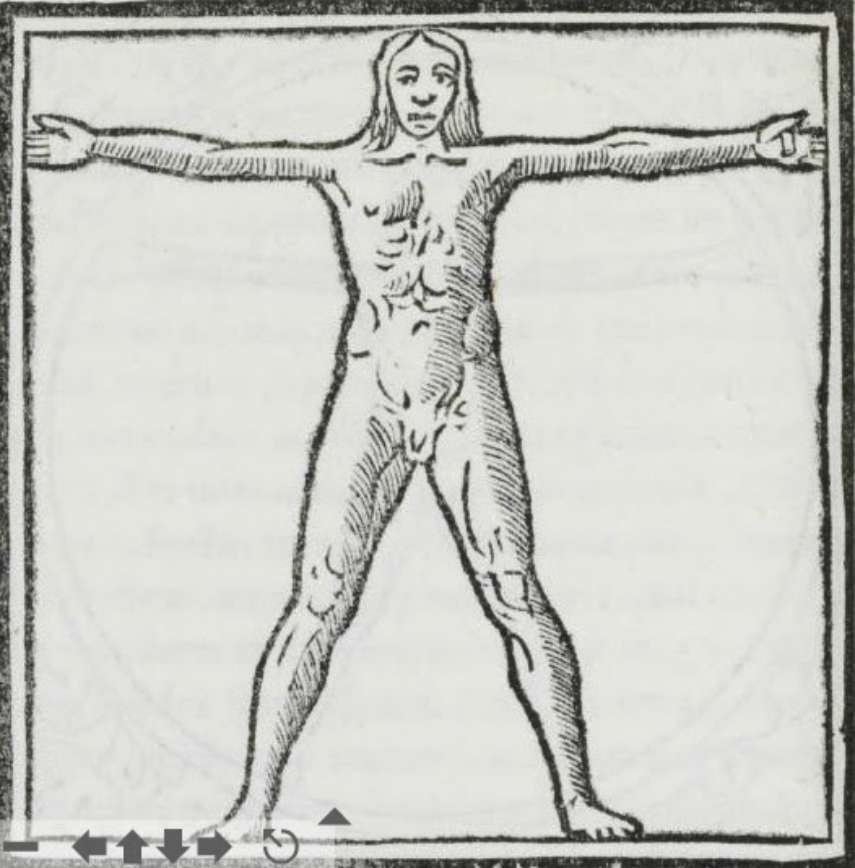
Vitruvius escreveu: "Para que um edifício seja belo, deve possuir simetria e proporções perfeitas como as que se encontram na natureza"..
A Idade Média e os construtores de catedrais
Na Idade Média, os construtores de catedrais utilizavam cinco medidas: o palmo, a palma, a canga, o pé e o côvado. A palma mede aproximadamente 7,6 dos nossos centímetros, a palma 12,4 cm, o palmo 20 cm, o pé 32,4 cm e o côvado 52,4 cm.
Estas medidas tinham uma relação constante entre si: a relação palmo a palmo era a mesma que a do pé ao palmo, ou do côvado ao pé. Um pedreiro ou carpinteiro experiente podia calcular cada uma destas medidas a partir de uma única, por construção geométrica.
O arquiteto responsável por uma obra trazia consigo uma bengala de medição com estas cinco medidas, geralmente baseadas nas suas próprias medidas. A bengala era utilizada como referência para as medições em todo o estaleiro. Mas atenção: estas medidas variavam de uma obra para outra, porque as medidas de um arquiteto podiam ser diferentes das de outro!
A aprendizagem de um destes ofícios de construção era muito demorada. O saber-fazer era transmitido ao aprendiz pelos seus mestres. O aprendiz tinha então de trabalhar em vários estaleiros e concluía a sua aprendizagem criando uma "obra-prima" que, uma vez aprovada pelos seus mestres artesãos, lhe permitia tornar-se um artesão de pleno direito e aprender e utilizar, em particular, estas medidas emblemáticas no seu ofício.
O companheirismo continua a ser praticado atualmente nos mais diversos domínios, desde a pedra e a madeira até à restauração e à pastelaria.
A Revolução Francesa e o nascimento do sistema métrico
O polegar, a palma da mão, o palmo, o empano, o pé e o côvado eram, portanto, medidas diretamente inspiradas nas medidas do corpo humano.
Mas, ao contrário das grandes épocas do Egito antigo e do mundo romano, durante as quais a humanidade tinha conseguido estabelecer um conjunto de medidas padrão numa vasta área, a Idade Média e o reinado da realeza viram florescer uma multiplicidade de pés e côvados diferentes: cada região, e mesmo cada cidade, tinha a sua própria medida oficial, de modo que, por altura da Revolução Francesa, não havia menos de cinquenta medidas de côvados diferentes no reino!
De facto, se medirmos o comprimento do nosso côvado e do côvado do nosso vizinho, é provável que encontremos comprimentos diferentes!
Os cientistas da revolução quiseram, por isso, estabelecer um novo sistema de medição baseado num padrão que permitisse que todos estivessem de acordo e desenvolveram o que hoje conhecemos como sistema métrico decimal.
O novo metro foi calculado como a décima milionésima parte de um quarto do meridiano terrestre. Este novo sistema de medição não tinha nada a ver com as medições humanas.
Em 1792, dois cientistas, Delambre e Méchain, foram encarregados pelo rei Luís XVI de medir a distância entre Dunquerke e Barcelona por triangulação, a fim de avaliar o comprimento do quarto do meridiano terrestre. Demoraram mais de sete anos a concluir a tarefa.
Hoje, graças aos modernos instrumentos de medição de que dispomos, sabemos que o resultado obtido por Delambre e Méchain, com os recursos disponíveis na altura, foi incrivelmente exato.
Entre 1796 e 1797, dezasseis metros-padrão foram colocados nos locais mais movimentados de Paris para promover o novo sistema métrico.

Em 1960, a definição do metro baseava-se num comprimento de onda: 1.650.763,73 vezes o comprimento de onda, no vácuo, da radiação laranja do átomo de crípton 86. Em 1983, na sequência de importantes trabalhos sobre a velocidade da luz e os relógios atómicos, o metro foi redefinido em termos da velocidade da luz, como sendo "o comprimento do caminho percorrido pela luz no vácuo durante 1/299.792.458 de segundo". É assim que esta definição se tornou abstrata e distante das medições humanas!
Apesar de o sistema métrico ser o sistema de medição mais utilizado atualmente no mundo, os hábitos humanos são difíceis de manter: quem nunca mediu as dimensões de uma sala em passos, ou o comprimento de um móvel com a largura da mão estendida (o empano)? Intuitivamente, continuamos a medir com o nosso próprio corpo!
Atualmente, os únicos países que não utilizam o sistema métrico são os Estados Unidos da América, a Libéria e a Birmânia. Estes países continuam a utilizar o chamado "sistema imperial de unidades". Este sistema, criado em 1824, destinava-se a ser utilizado em todo o Império Britânico. Continua a ser utilizado em indústrias como a aeronáutica e a multimédia. (Um ecrã de computador ou de televisão é medido em polegadas!)
O retângulo de ouro
Voltemos ao nosso retângulo áureo: qual poderá ser a relação entre a corda de treze nós (o triângulo egípcio), o pé e o côvado? Observe atentamente a figura abaixo:
A relação entre o lado "5" e o lado "3" do triângulo egípcio é a mesma que existe entre o côvado e o pé!
O mesmo se passa com o pé e o palmo, o palmo e a palma, e a palma e a palma.
Esta relação, ou seja, a divisão do maior comprimento pelo menor, foi denominada "número de ouro" no início do século XX.
Um retângulo dourado é, portanto, um retângulo cuja relação entre o comprimento e a altura representa o Número de Ouro, ou seja, 1,618.

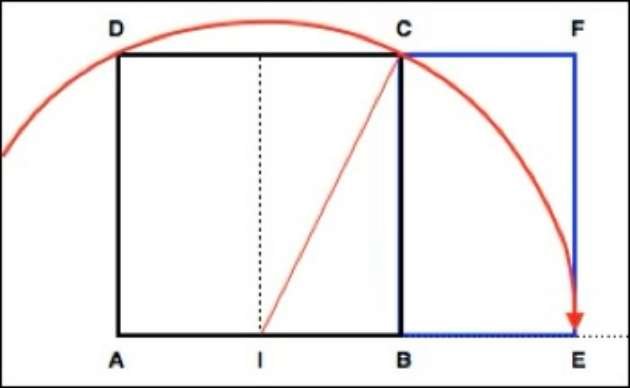
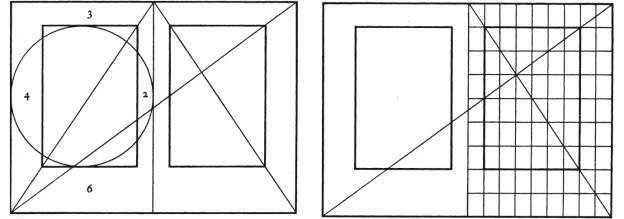
O esquema abaixo mostra as etapas da construção de um retângulo áureo: este é obtido a partir de um quadrado ABCD. Um arco de circunferência de centro I (o ponto médio de AB) e raio IC intersecta a reta AB no ponto E.
O retângulo AEFD é um retângulo áureo. A razão entre a sua largura e a sua altura é 1,618, o valor da razão áurea.
AE/EF = (1 √5)/2 = 1,618
O novo retângulo criado BEFC é também um retângulo áureo, ou seja, EF/BE = 1,618
Veremos mais tarde que, sem necessariamente nos apercebermos, estamos rodeados de rectângulos de ouro! Vamos descobri-los juntos.
A experiência de Gustav Fechner
Gustav Fechner (1801-1887) foi um filósofo e psicólogo alemão, conhecido como um dos fundadores da psicologia experimental.
Pediu aos seus alunos que escolhessem o mais harmonioso de dez rectângulos. Sete em cada dez alunos escolheram o retângulo cujas proporções correspondiam ao Retângulo de Ouro!

Será que os alunos de Gustav Fechner reconheceram intuitivamente as proporções do corpo humano no retângulo escolhido? Pelo menos, era isso que o psicólogo queria provar com esta experiência.
A primeira definição da Proporção Áurea
A Proporção Áurea nem sempre teve este nome, mas foi conhecida por outros nomes durante centenas, se não milhares, de anos.
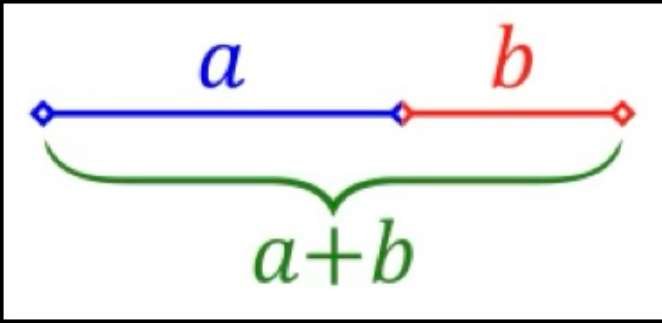
Euclides, um antigo matemático grego (cerca de 300 a.C.), definiu a divisão de um segmento de reta em "razão extrema e média" (ou seja, em dois segmentos desiguais) quando a razão entre o comprimento total e o segmento mais longo é igual à razão entre o segmento mais longo e o mais curto. Na sua opinião, esta é a forma mais harmoniosa de dividir um segmento de reta em duas partes desiguais.
Vimos acima que os construtores de catedrais conheciam a relação constante entre o palmo, o palmo, o palmo, o palmo, o pé e o côvado. Esta relação era uma espécie de segredo comercial. Só os iniciados sabiam como a utilizar.
A sequência de Fibonacci
Em 1202, o matemático Leonardo Fibonacci, também conhecido como Leonardo de Pisa, publicou um livro no qual descrevia a sua descoberta de uma sequência algébrica que hoje tem o seu nome, a "sequência de Fibonacci". Na sua época, atribui-se a Leonardo Fibonacci a introdução da numeração indo-arábica (1,2,3,4,5,6,7,8,9) e do zero, que não existia na numeração romana, na Europa.
Diz a lenda que Fibonacci descobriu esta sequência matemática ao examinar a reprodução de pares de coelhos; um par de coelhos gera outro par, que por sua vez gera dois pares de coelhos, que por sua vez têm vários bebés, e assim por diante..
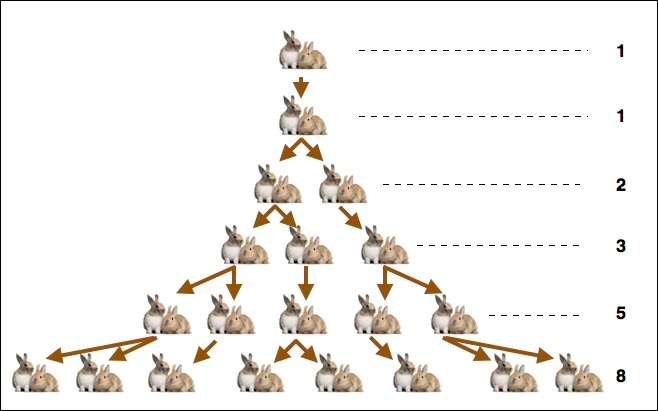
Vejamos mais de perto esta sequência numérica: é uma sequência de números inteiros em que cada elemento é a soma dos dois termos que o precedem. O primeiro destes termos é zero e o seguinte é 1.
A sequência escreve-se da seguinte forma; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 e assim por diante. De facto, 144, retirado ao acaso desta sequência, é a soma de 55 e 89, tal como 5 é a soma de 3 e 2.
Se dividirmos agora um dos termos da sequência pelo termo anterior, por exemplo 144 por 89, obtemos .... 1.618 !!!
Existe, portanto, uma ligação evidente entre a sequência de Fibonacci e as 5 medidas emblemáticas deduzidas das proporções do corpo humano, utilizadas na construção de edifícios sagrados na Idade Média.
Estas medidas eram subdivididas em linhas, representando uma linha o comprimento de um grão de cevada. A palma da mão valia 34 linhas, o palmo 55, o empano 89, o pé 144 e o côvado 233! Encontramos esta sequência de números na sequência de Fibonacci! No entanto, parece que o próprio Fibonacci não fez esta ligação na altura, o que pode parecer lógico; apenas os arquitectos e os jornaleiros utilizavam o sistema de medidas em vigor na altura, e Leonardo Fibonacci não era um deles!
A Divina Proporção
Foi preciso esperar até ao século XV para encontrar um vestígio oficial desta proporção muito especial. Em 1496, Leonardo da Vinci ilustrou um livro de um famoso matemático contemporâneo, Luca Pacioli. Este livro, que descreve os poliedros (formas geométricas tridimensionais) e trata da proporção aplicada à geometria, à arquitetura e às artes, chama-se "Divina proporção". Luca Pacioli compara as proporções destas figuras geométricas às proporções humanas e, portanto, divinas, daí o título do seu livro.

Finalmente, no século XIX, o filósofo e matemático alemão Adolf Zeising falou da "secção áurea" (Goldener Schnitt) ao analisar a estrutura do esqueleto humano.
No início do século XX, Matila Ghyka, um diplomata romeno apaixonado pela estética, inspirou-se no trabalho de Adolf Zeising e chamou a esta relação a "Proporção Áurea". O seu livro "Le nombre d'Or" foi um grande sucesso junto de muitos designers e filósofos.
A fórmula matemática para este número é (1 √5)/2, um valor próximo de 1,618. Os matemáticos deram a letra grega φ (pronuncia-se "phi") como símbolo da proporção áurea, em memória de Fídias, o arquiteto que decorou o famoso Partenon em Atenas.
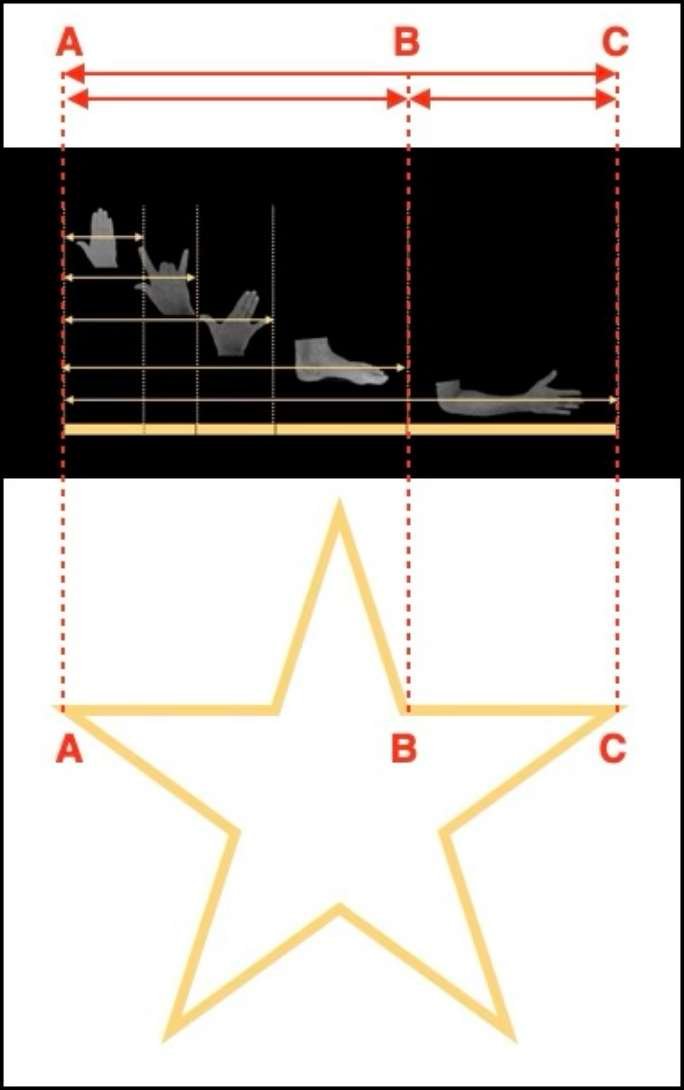
Se tivéssemos de dar uma definição simples e pictórica da proporção áurea, esta seria o resultado da divisão do comprimento de um côvado pelo comprimento de um pé, ou do comprimento de um antebraço pelo comprimento de uma mão. Esta proporção encontra-se em muitas partes do corpo humano e também em muitas figuras geométricas, como a estrela de cinco pontas ou as figuras da geometria euclidiana.
Na figura abaixo, podemos ver que a relação entre o côvado e o pé é idêntica à relação entre os segmentos AC e AB, e os segmentos AB e BC da estrela de cinco pontas.
Não é de estranhar, portanto, que este número, utilizado por figuras religiosas, arquitectos e cientistas da época, se tenha tornado um mito. Note-se também a importância simbólica da estrela de 5 pontas na maioria das religiões e o facto de a encontrarmos em muitas bandeiras nacionais.
O Número de Ouro e o corpo humano
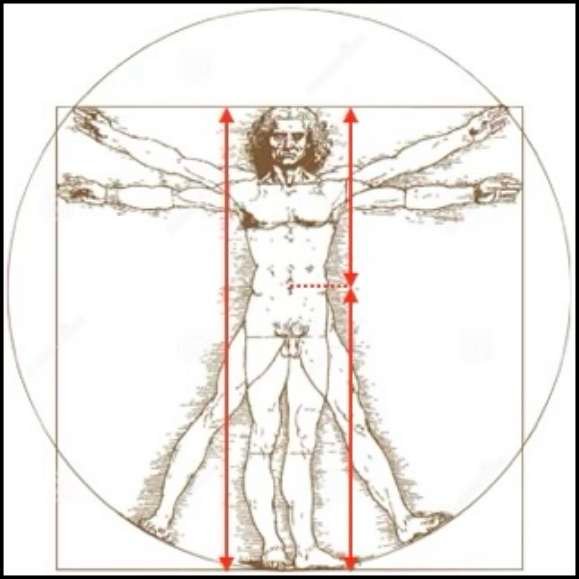
Faça esta experiência: sabe a sua altura. Divida a sua altura por este famoso Número de Ouro e meça o resultado desta divisão a partir do chão... encontrou a altura do seu umbigo!
Agora, meça o comprimento desde a ponta do seu cotovelo até à extremidade da sua mão estendida. Divida o resultado por 1,618 e obterá o comprimento desde a ponta do cotovelo até à articulação do pulso.
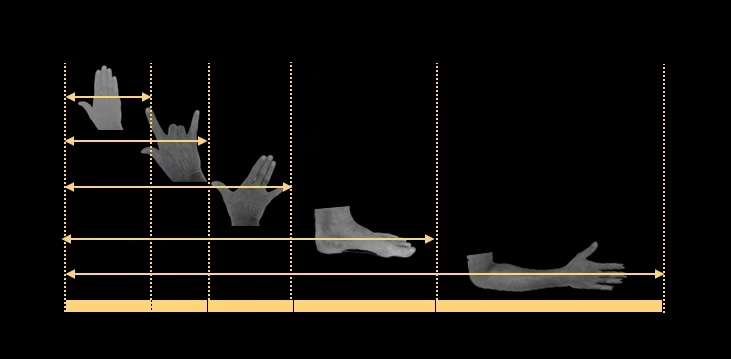
Se considerarmos as três falanges do dedo médio e o metacarpo, o osso que se estende das falanges ao pulso, a progressão do seu tamanho é idêntica à das cinco medidas utilizadas pelos construtores de catedrais! (palma, palma, jugo, pé e côvado)
Mas todos nós temos medidas diferentes, e a proporção dos membros de uma pessoa não é exatamente a mesma, com aproximação ao milímetro, que a proporção dos membros de outra pessoa!
Se pegarmos nas medidas do nosso pé e do nosso côvado e dividirmos o comprimento do nosso côvado pelo comprimento do nosso pé, não obteremos necessariamente 1,618, mas algo do género.
O sistema concebido pelos construtores de catedrais era um sistema geométrico inspirado nas medidas do corpo humano. Representava um padrão local, ou norma de construção, para que dois pedreiros pudessem cortar dois blocos de pedra perfeitamente idênticos num determinado dia ou dois anos depois. Imaginemos o contrário, cada pedreiro poderia cortar um bloco de pedra do tamanho do seu próprio côvado: todos os blocos seriam diferentes e a construção do monumento tornar-se-ia impossível!
Le Corbusier e o Modulor
Mais perto do nosso tempo, após a Segunda Guerra Mundial, o arquiteto franco-suíço Charles-Édouard Jeanneret-Gris, conhecido como "Le Corbusier", utilizou este sistema proporcional para estruturar os edifícios que construía, tanto em termos de proporções interiores como exteriores, com o objetivo de garantir que os seus habitantes pudessem viver em volumes harmoniosos que correspondessem às proporções humanas.
Deu-lhe um nome: o Modulor. Baseado nas proporções do corpo humano, o Modulor era uma ferramenta de normalização que permitia a todos os profissionais, dos arquitectos aos marceneiros, conceber rapidamente volumes, portas e mobiliário com proporções humanas harmoniosas.
O esboço do arquiteto abaixo define a relação entre o tamanho do mobiliário e as diferentes posturas do corpo humano.
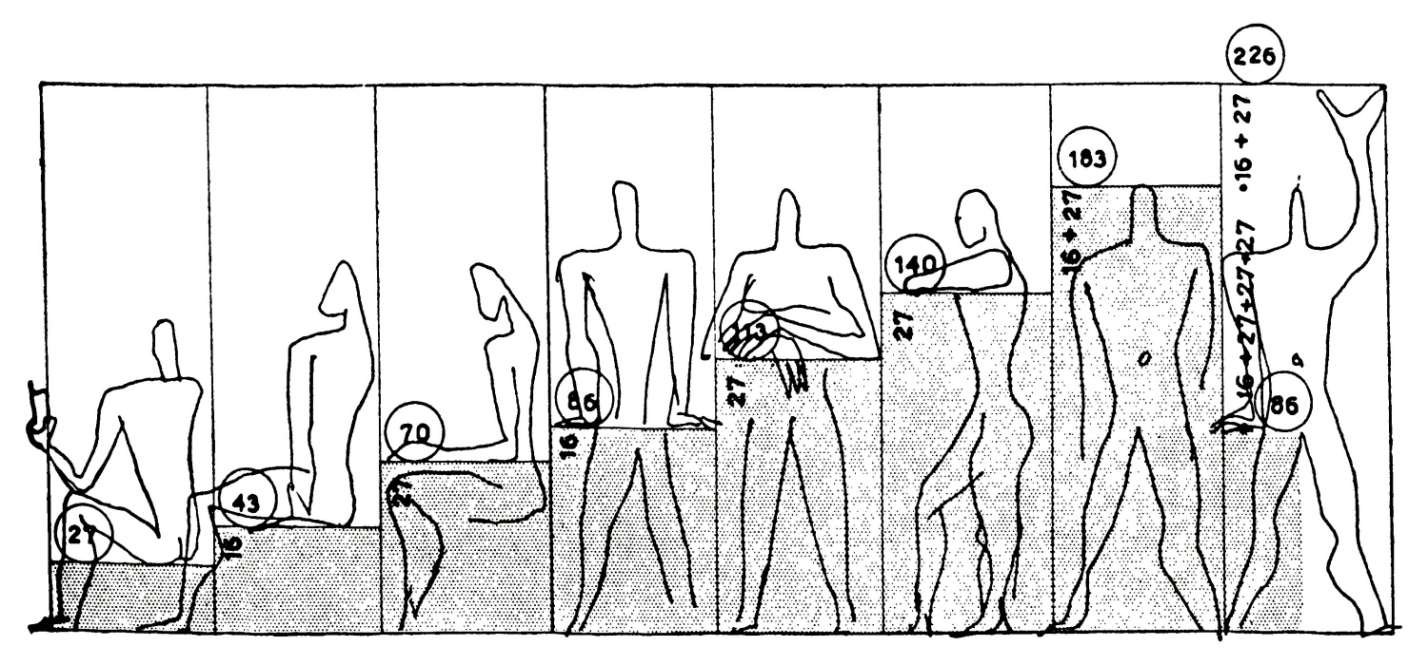
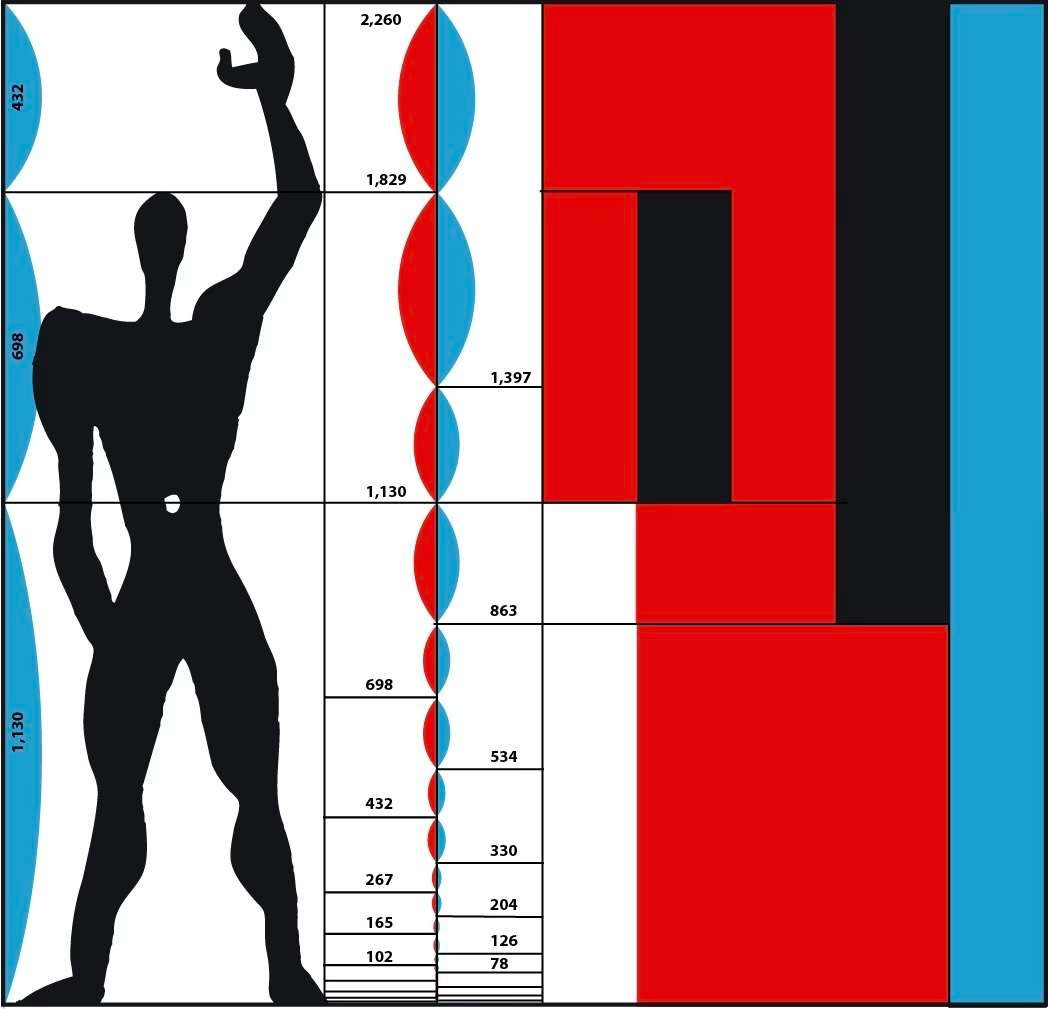
Desde o início do século XX, os pintores também utilizaram deliberadamente esta técnica para estruturar as suas obras, mesmo que as dimensões externas dos seus quadros não fossem as de um retângulo dourado. Os centros de interesse e as linhas de força dos seus quadros foram muitas vezes colocados em posições calculadas com base neste princípio.
Hoje em dia, estas proporções são também utilizadas de forma consciente e deliberada por fotógrafos de arte, arquitectos, escultores, artesãos e designers.
Linhas de controlo
Uma "linha de controlo" é a estrutura geométrica que serve de base a um desenho para o equilibrar. O desenho pode ser de um edifício, um esboço de uma escultura, um jardim ou um quadro.
Como disse o arquiteto Le Corbusier: "A linha de regulação não contribui com ideias poéticas ou líricas; não inspira de modo algum o tema; não é criativa; equilibra. É um problema de pura plasticidade".

Eis um exemplo muito simples de estruturação regulamentar: pense nas riscas dos cadernos escolares, que serviam para determinar uma margem sobre a qual se podia alinhar a página de escrita e para calibrar as palavras e as frases de modo a facilitar a sua leitura. Esta estrutura não tem nada a ver com o sentido do texto. Representava uma formatação, um alinhamento de parágrafos e frases, e permitia uma leitura mais clara.

Este desenho de Le Corbusier explica o próprio princípio da planta reguladora: a primeira perceção que temos de um edifício é o seu volume puro. A partir do momento em que se faz uma abertura numa parede (uma janela, uma porta), criam-se relações de comprimento.
a planta de regulação revela os princípios geométricos que regem a composição arquitetónica, tornando-a legível e compreensível.
Os traçados reguladores são utilizados desde a antiguidade para desenhar a estrutura de um edifício no solo e em volume, e também para o orientar em relação ao sol ou mesmo às estrelas.
Abaixo, a planta baixa e a fachada da Villa Rotonda em Veneto, construída por volta de 1570 pelo arquiteto Andrea Palladio. À direita, uma linha de regulação determina a estrutura geral do edifício, bem como o seu ritmo. Estas linhas estruturais servem para dar equilíbrio e uma dinâmica clara ao edifício. A composição geral baseia-se em círculos concêntricos e quadrados.
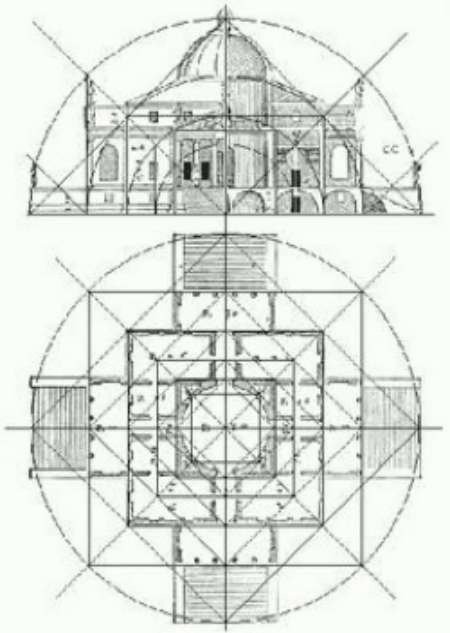
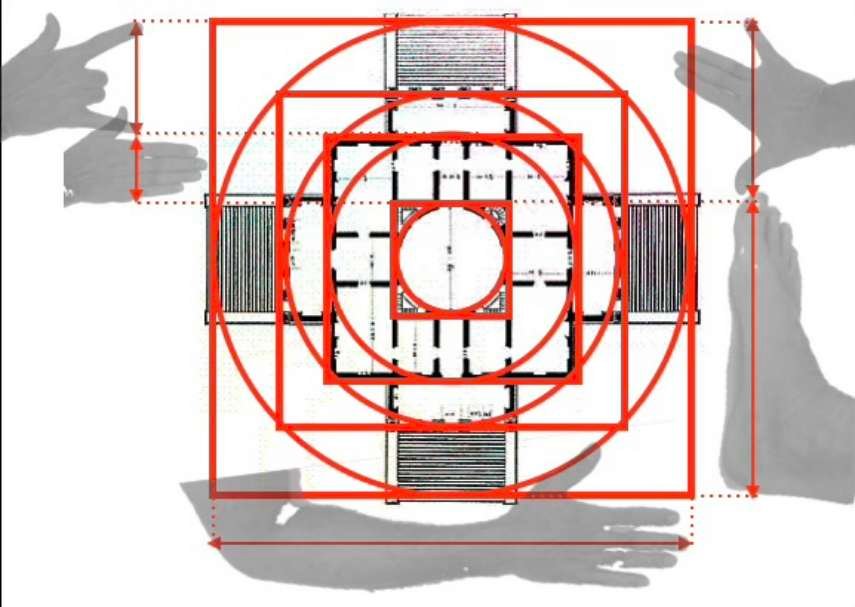
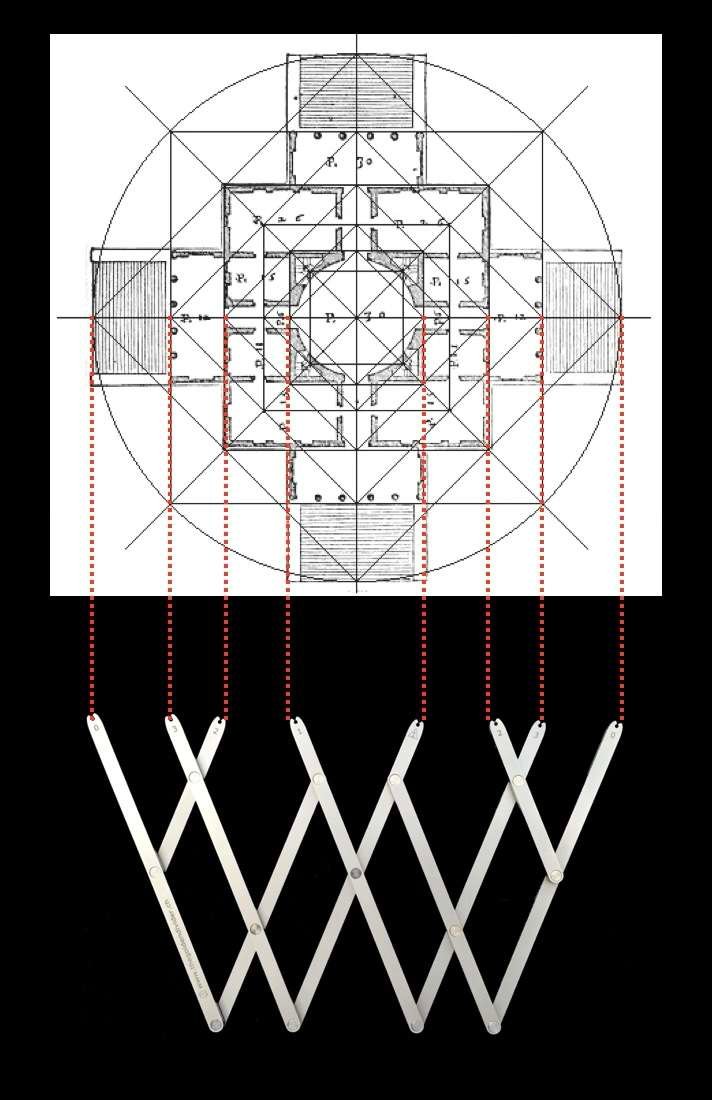
Se observarmos mais atentamente a forma como estes quadrados e círculos concêntricos estão distribuídos, verificamos que as relações entre estas diferentes figuras geométricas correspondem proporcionalmente às relações entre a palma da mão, a palma da mão, o palmo, o pé e o côvado.
As plantas e a fachada do edifício têm, portanto, proporções que encontramos no corpo humano, e é sem dúvida por isso que inconscientemente o achamos harmonioso.
A linha de regulação utilizada pelo arquiteto não é o desenho do edifício, mas serve para o proporcionalizar e, assim, dar-lhe um significado e um alcance particulares.
Se é certo que as linhas de regulação são utilizadas na arquitetura desde a Antiguidade, a sua utilização na pintura remonta à época em que os pintores puderam compreender e dominar a perspetiva, ou seja, no início do Renascimento.
As linhas reguladoras foram e continuam a ser utilizadas em muitos domínios: abaixo, uma linha utilizada na tipografia, datada do século XIII, que regula a posição do texto em relação ao tamanho da página. Este tipo de linha ainda é utilizado na computação gráfica.
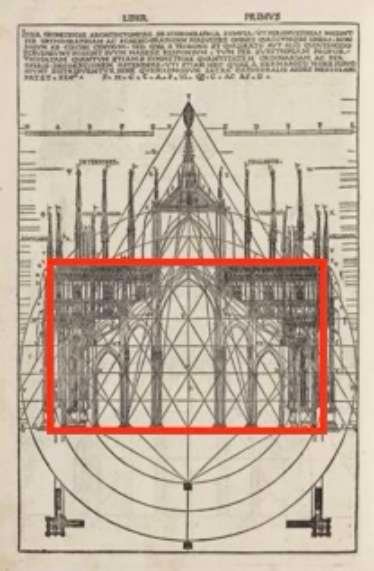
A figura da esquerda mostra uma análise da fachada do Duomo, a catedral de Milão, utilizando um esquema regular baseado em círculos concêntricos e triângulos.
A planta baixa mostra as proporções de um retângulo dourado e o símbolo da cruz, no centro da qual se encontra a torre do Duomo.
Quando se analisa a planta baixa e a fachada da catedral de Reims, mostrada abaixo no centro, é difícil imaginar que o arquiteto não se tenha inspirado em figuras geométricas e símbolos religiosos ocultos ao projetar e construir este edifício.
É certo que utilizou um traçado regular.

Note-se, de passagem, que encontramos o famoso retângulo dourado nas dimensões das fachadas dos dois edifícios religiosos. E este retângulo é tanto mais familiar quanto nos faz lembrar as proporções do rosto humano.
