Analysis of a work of art

The Golden Number and Painting

We saw above that human proportions were at the origin of a system of measurements used since antiquity. The relationship between these measurements has been called the Golden Ratio, and we find traces of it in fields as varied as mathematics, geometry, architecture and typography.

This is also the case in painting; from the moment painters mastered perspective, and pictorial representation became more realistic, painters structured their works using the measurement system of their time.

In the Middle Ages, painting was above all meaningful, i.e. symbolic. The size of figures was a function of their importance and dignity. The image opposite is an example of inverted perspective, where the less important characters are smaller than the main subjects, even if they are placed in the foreground.

From the Renaissance onwards, a more realistic perspective appeared in the paintings of the masters of the time. Fra Angelico's (1400 - 1455) depiction of the Annunciation shows that the principles of perspective had been acquired, and that the figures are of a realistic size in relation to the buildings.

In the decades that followed, painters used the existing system of measurement to structure their works: figures were placed in precise locations, known today as focal points.

Paul Veronese painted the Wedding at Cana around 1562. Perspective is perfectly mastered. The groups of characters are thoughtfully arranged, and we witness a veritable cinematic mise-en-scène, framed on very strict geometric principles; the grid superimposed on Veronese's painting below, allows us to imagine this geometrically-based mise-en-scène.

The general mastery of these representational effects also enabled the painter to "see big". The size of works from this period has nothing in common with the illuminations of the Middle Ages: the painting measures almost 7 by 10 meters!

Analyzing the structure of an Italian Renaissance painting

We now know enough about the system of measurements that preceded the decimal metric system to analyze the structure of one of the most famous paintings of the Italian Renaissance, the "Birth of Venus", painted by Sandro Botticelli around 1485.

The Birth of Venus

Venus is born from a shell. On her left are Zephyr and Chloris. Zephyr is the son of Aeolus, god of the winds, and Chloris, his wife, is a nymph who reigns over the empire of flowers. They blow on Venus as if to undress her or dry her from the water in which she was born, but also to purify her and cover her with flowers. To Venus' right is an "hour", daughter of Zeus, one of the mistresses of time. She seems intent on covering Venus with a cloth adorned with flowers to hide her nakedness, or to warm her.

Botticelli's inspiration for Venus was Simonetta Cattaneo, one of Florence's most beautiful women, wife of the wealthy merchant Marco Vespucci and possibly mistress of Giuliano de Medici, whose brother Lorenzo ruled the city at the time. Simonetta died very young, and the painter used her as a posthumous model in many of his paintings. A platonic lover of the beautiful woman, Botticelli wanted to be buried next to her when she died. Both their bodies now lie in the Ognissanti church in Florence.

Analysis of the positioning of the figures in the painting

Observe how these figures are positioned in the painting. Also note the horizon line, the boundary between sea and sky. It is not in the middle of the painting's height, just as Venus, the work's central figure, is not exactly in the center of the painting.

The painting measures 2.78 meters wide by 1.72 meters high. These measurements may seem abstract, but let's not forget that in those days, we measured in feet and cubits.

We know today that the cubit measured between 53 and 55 cm and the foot between 33 and 36 cm. We also know that painters used to divide the height of their canvas into eights, in order to square it and then place the main elements of their paintings.

If we divide the height of this painting by 8, we get 21.5 cm. And if we divide its width by 8, we find 34.7 cm.

21.5 cm seems to be the measure of the span and 34.7 cm that of the foot, measures used at the time. Perhaps these were Sandro Botticelli's own measurements?

At the time, the painting must have measured 5 x 3 cubits, or 8 x 5 feet, or 13 x 8 empans!

Squaring the painting in contemporary measurements

Let's start by squaring the painting with a regular grid of squares measuring, at the scale of the painting, 35 cm on a side, the length of a foot. We see that the various figures in the painting are distributed as follows:

Zephyr and Chloris occupy a rectangle 3 squares wide by 5 high on the left of the painting, and Hour, daughter of Zeus, the same rectangle on her right.

Venus, for her part, fits into a rectangle in the middle of the painting, 2 squares wide by 5 high. The horizon line seems to coincide with one of the grid lines, and the shell that gives birth to Venus fits into a rectangle 3 squares wide by 2 high.

You'll recall that we divided the width of the painting by 8 above; let's now square it with a regular grid of 21.5 cm squares, dividing its height by 8.

21.5 cm is the approximate length of the span.

Zephyr and Chloris occupy a rectangle 5 squares wide by 8 high on the left of the painting, and Hour, daughter of Zeus, the same rectangle on her right.

Venus fits into a rectangle in the middle of the painting, 3 squares wide by 8 high. What's more, she appears to be centered on one of the lines of this new grid. The horizon line coincides with one of the lines of this grid, and the shell is contained within a rectangle 6 squares wide by 3 high.

We can see that the layout of the painting (horizon line, location of the various characters) is virtually identical, whether the painting is divided into 5x8 or 8x13 squares. The 8x13 division just seems more "refined".

Note also that 3, 5, 8 and 13 are among the first numbers in the famous Fibonacci sequence, and that dividing 8 by 5, and 13 by 8, yields a value ever closer to 1,618!

A regulating layout based on the Golden Ratio

If we were to use today's calculators and computers to draw a regulating line based on the Golden Ratio, we'd proceed as follows: take a rectangle of the same format as the one in Botticelli's painting, and divide its width by 1.618: we obtain the figure below. The total width of the rectangle divided by 1.618 allows us to draw a vertical line dividing the rectangle into a square on the left, and a rectangle on the right. Let's continue dividing the small rectangle in the same way twice in a row.

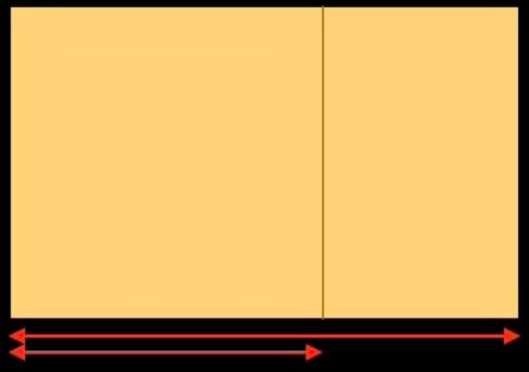
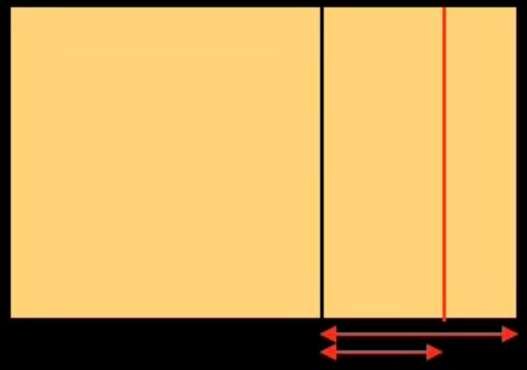
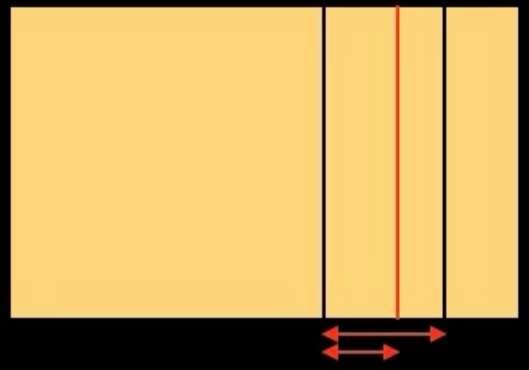
We've obtained three subdivisions on the right-hand side of the initial rectangle. Let's perform the same operation on the left-hand side: we obtain the figure below on the left. We've divided the initial rectangle vertically 6 times. Now we'll divide it horizontally. We obtain the figure below on the right.

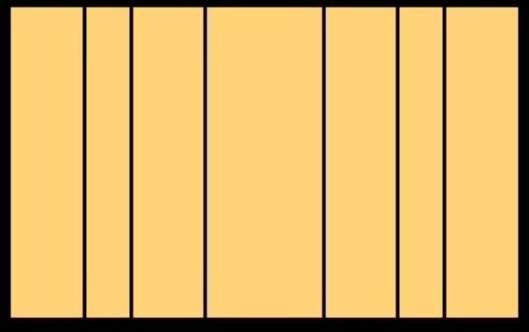
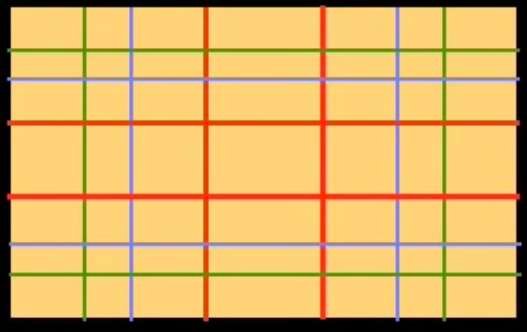
The red lines represent the first division of the width and height of the initial rectangle by the Golden Number. We'll call this the primary division.

The blue lines represent a secondary division (i.e. the division of the rectangles created by the first division), and the green lines a tertiary division, i.e. the division of the rectangles created by the second division.

We'll now superimpose this modern "regulator plot" on Botticelli's painting, and compare it with the plots obtained by the two previous 5x8 and 8x13 grids.

5x8 grid

(Measure in feet)

8x13 grid

(Measure in empans)

Regular layout awarded by the Golden Divider for Arts

We can see that the internal division of the picture is virtually identical: the horizon line is more or less in the same place, and the figures and groups of figures in the picture occupy the same surfaces.

What can we deduce from this?

We know that Botticelli had neither a calculator nor a "tape measure" at the time. So he could only place the focal points of his painting using his own measurements.

Botticelli had learned his art from a painter-monk named Fra Filippo Lippi, who had certainly taught him how to structure a painting symbolically, i.e. using human, and therefore divine, measurements and proportions. This know-how was a trade secret, just like that of the master builders, and was passed down from master to pupil, from generation to generation.

With regard to the regulating layout of Botticelli's painting, it is by no means certain that the painter knew the Fibonacci sequence, or even that he knew the Golden Number. We can't imagine Sandro Botticelli taking out a calculator - which didn't exist at the time - and dividing the height and width of his painting by (1 √5)/2!

But we know today that by dividing the height of his canvas by 8, and using the measurements of his time, the result obtained was practically the same. This manufacturing secret, certainly of religious inspiration, was therefore accessible through simple geometry: a string is enough to divide a length into 2, then 4 and 8. In the same way, the user of a 13-knot string to check a right angle has no idea of the historical, geometrical and quasi-mystical significance of the tool he's handling.

The notion of the Golden Number was inherent in the measurement system used by our ancestors: they used it without having to know it. In fact, the combination of measures such as the cubit, the foot and the empan made the "golden" proportions appear "mathematically".

We unconsciously find familiar, human proportions in Botticelli's painting, and it's no doubt for this reason that the work seems balanced to us.

Compare the placement of the horizon line in relation to the height of the picture and the position of the wrist joint in a human forearm. The various groups making up the picture are also arranged according to the same logic.

According to the cathedral builders' system of measurement, if the length of the cubit is the distance from the elbow to the tip of the outstretched hand, then the length of the foot would be that of the forearm without the length of the hand, and the length of the hand would be equivalent to that of the span, i.e. the width of the hand with fingers spread.

Structural analysis of paintings from different periods

Diego Velasquez - Venus with mirror - 1647

Observe the arrangement of Venus' body, which fits into an elongated rectangle occupying two-thirds of the bottom of the painting (dotted line above). Her bust fits into a rectangle, marked here in red, in the lower right-hand corner of the painting. An identical rectangle frames the cherub at top left, in diagonal symmetry.

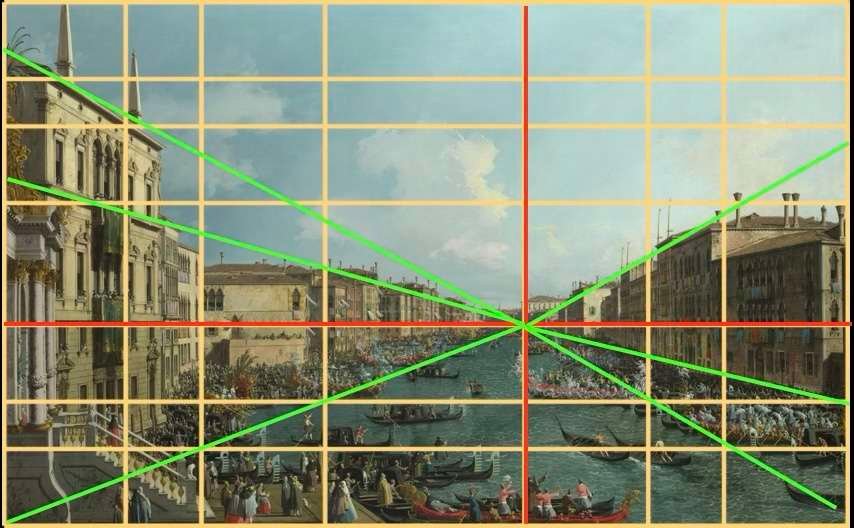
Canaletto - Regatta on the Grand Canal - 1740

Observe here the placement of the horizon line, and the vanishing point of the painting located on it, at the intersection of the two red lines. All the vanishing lines, in green, converge on this single vanishing point.

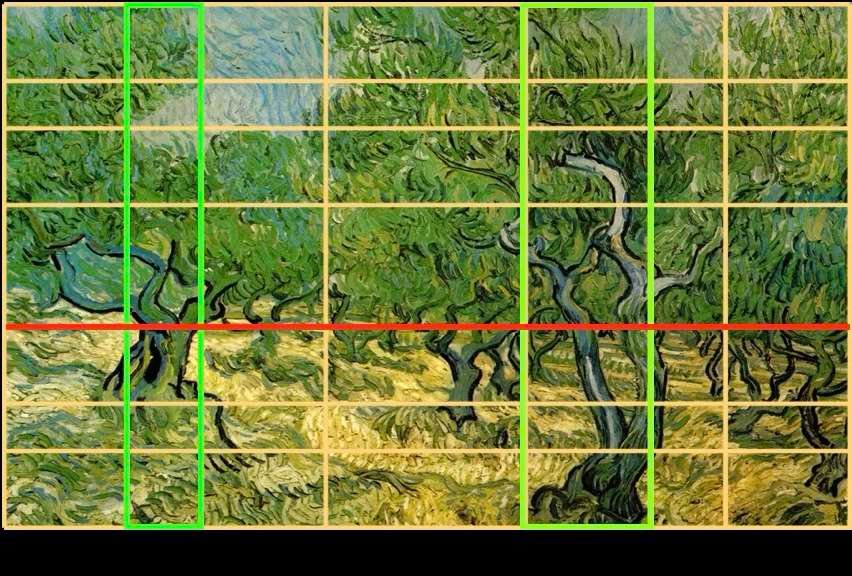
Vincent Van Gogh - The olive trees - circa 1889

The horizon line, shown here in red, delimits the ground from the foliage of the olive trees. The two main tree trunks, in green, are at the center of two rectangles delimited by the arrows below the painting. While each tree is symmetrical in itself, the asymmetry of the two trees gives the picture a harmonious dynamic.

Ferdinand Hodler - The Maggia delta before sunrise - 1893

The "division" of the picture becomes evident here thanks to the structural grid: the elongated top rectangle delimits the mountain range, the middle one the ice and the bottom one the clear water. The horizon line, in red, is delimited by the two tall rectangles.

Below, two paintings by masters whose external proportions differ from those of the golden rectangle. However, the internal structure of these paintings suggests that the golden ratio has been used, whether consciously or not.

Leonardo da Vinci- The Annunciation - 1472

This painting is not in the format of a golden rectangle, but the internal division of its structure, in red, established according to the golden rule, reveals four rectangles whose lines delimit the horizon line, the angle of the building and the respective positioning of the figures.

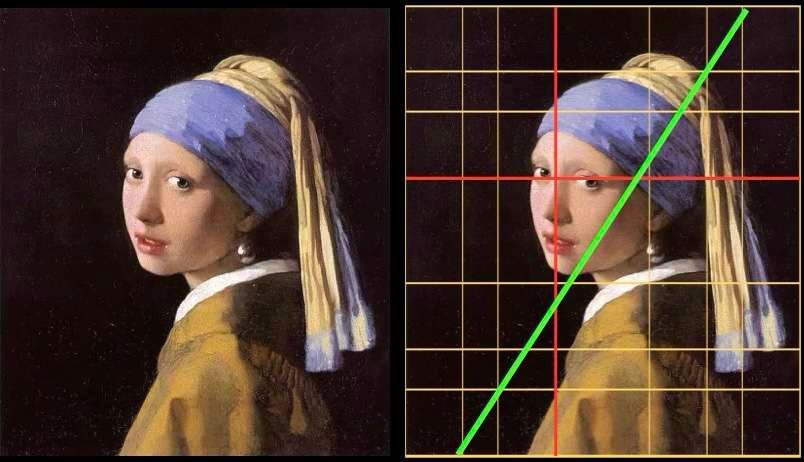
Johannes Vermeer - Girl with a Pearl - 1665

A quick glance at the painting suggests that the young girl's face is in the center. But if we superimpose a structural grid based on the golden ratio, we see the specific positioning of the girl's face: the red lines precisely determine the alignment of her eyes and the vertical axis of her face. A diagonal line, in green on the image, delimits light and shadow.

The Golden Number and industrial design

There is undoubtedly a relationship between aesthetics and functionality: in other words, what is beautiful is functional, and everything that is functional is beautiful, just as in the human body. The following examples illustrate how the Golden Number signals its presence on a daily basis.
Many of the objects in our daily lives have proportions that approach those of a Golden Rectangle, and therefore of the human body.

The format of certain books, a radio, a perfume box or the relationship between the dimensions of a window are striking examples. You'll notice that many windows have the proportions of the Golden Rectangle, and it's not surprising that they should; the habit was established of giving common windows the following dimensions: three feet wide by three cubits high, the perfect proportions of a Golden Rectangle!

Below, a regular pattern has been superimposed on silhouettes of boats, planes, cars and even handguns. The apparent asymmetry of the volumes is called dynamic symmetry.

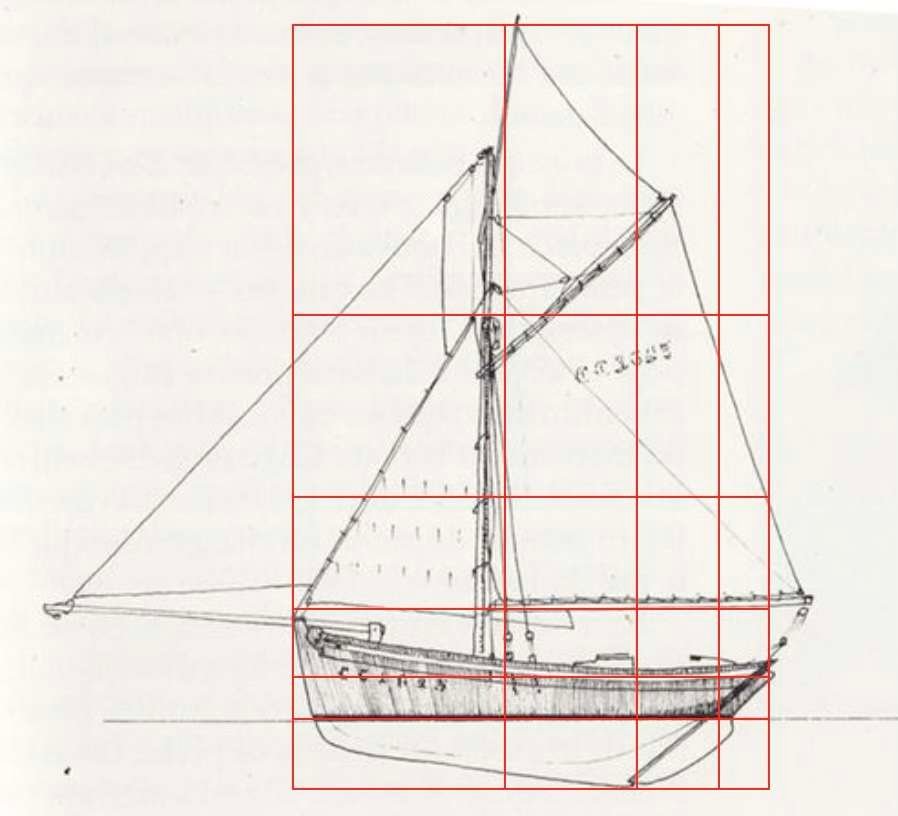
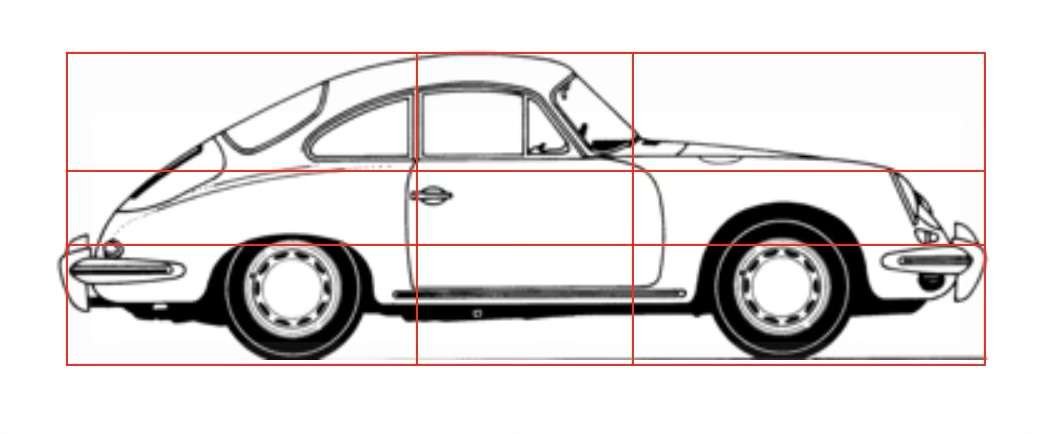
The proportions used in marine, aeronautical, automotive and military construction show that aesthetics and functionality are inextricably linked.

The Golden Number and architecture

The Golden Number inspired the architecture of the ancient, medieval and Renaissance periods, thanks, as we've seen, to a system of measurements based on this concept.

The Pyramid of Khufu, the Parthenon in Athens, Notre Dame Cathedral in Paris, as well as most of the sacred buildings constructed in Europe in the Middle Ages, the Great Mosque of Kairouan in Tunisia and the Taj Mahal in India are all recognized examples.

But is the Golden Number still used today in this discipline?

After the Second World War, the Franco-Swiss architect Charles-Édouard Jeanneret-Gris, known as Le Corbusier (1887 - 1965), took up the theories of the Roman architect Vitruvius, seeking to adapt urban planning, architecture and even furniture to human morphology.

In 1945, he developed an architectural concept known as the Modulor, which standardized the human environment according to its own proportions.

The name "Modulor" is a contraction of "module" and "golden number".

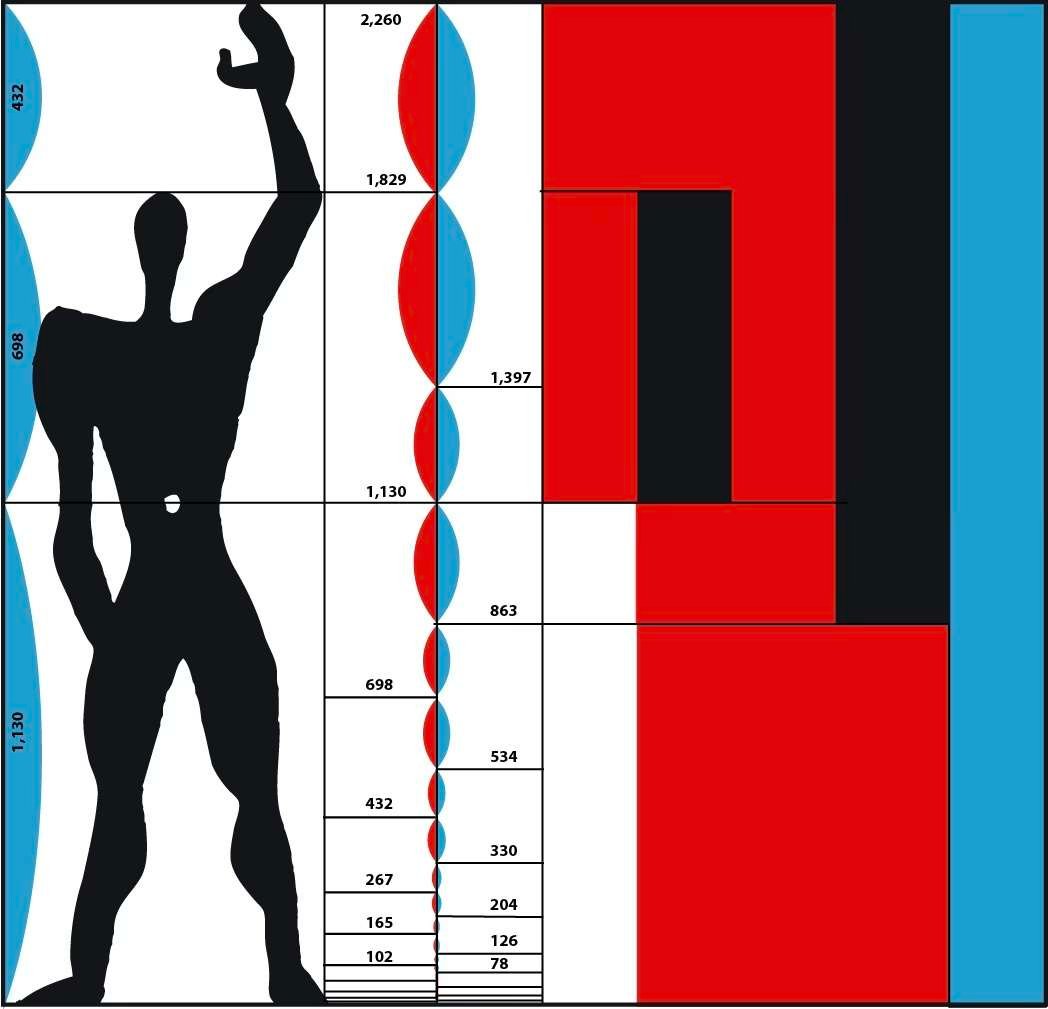
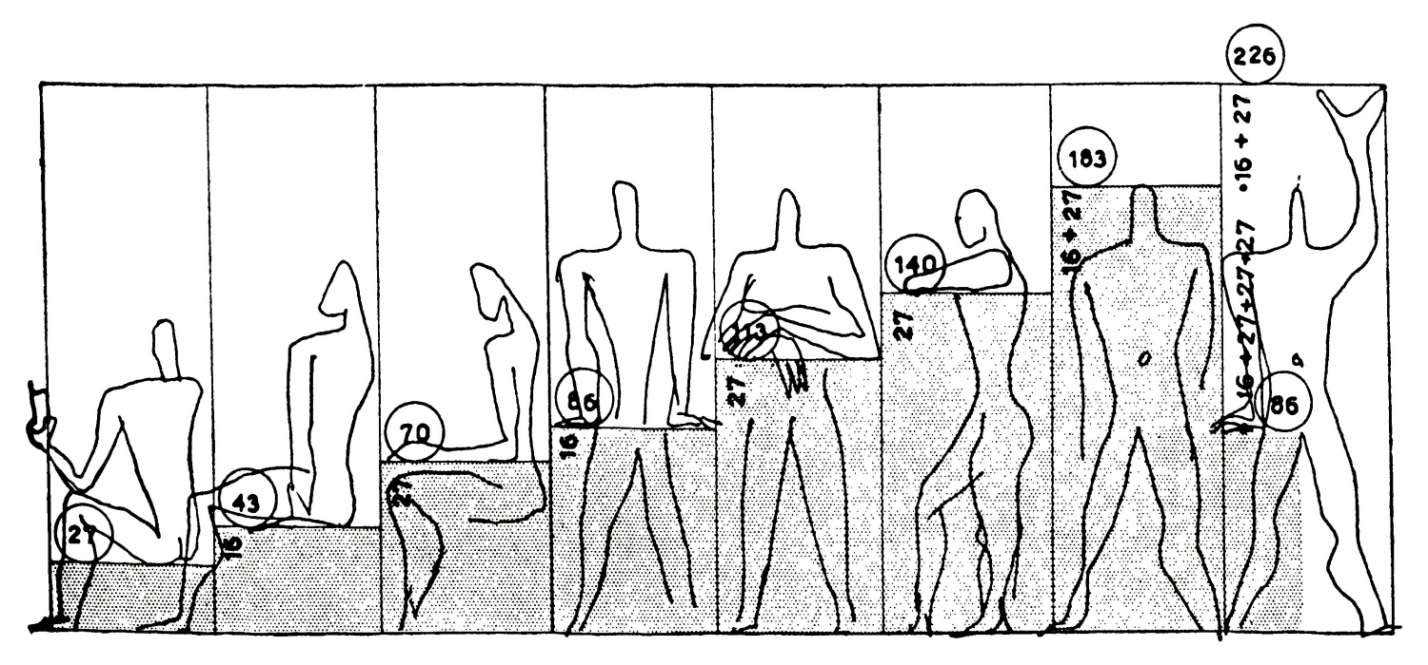
Although Le Corbusier's projects are relatively few in number - the best-known of his seventeen sites being the Tokyo National Museum of Western Art (1959), the city of Chandigarh in India (1951), La villa Savoye (1928-1931), the Cité Radieuse in Marseille (1952) and the Chapel of Notre-Dame-du-Haut in Ronchamp (1953-1955) - he nevertheless influenced a whole generation of architects worldwide.

The idea of designing housing and interior architecture compatible with human proportions still appeals to a large number of architects of all nationalities.

Have we found the Golden Rectangle?

Yes, because we're literally surrounded by it, if we look hard enough! Of course, we no longer measure our surroundings in feet and cubits, and the decimal metric system has certainly, by virtue of being so abstract and different from the human body, muddied the waters in the way we perceive and evaluate our environment.

But the habits acquired over the centuries have remained; the evaluation of a human figure, a work of architecture, a painting or even an object still involves an unconscious comparison with human proportions.

The Golden Ratio, that special relationship between the height and width of a golden rectangle, is unconsciously found in a hand or a face, which, more or less, fit into this geometric figure.

Our idea of harmony and beauty is inseparable from our perception of the human body. It is undoubtedly this unconscious analysis that we constantly make that provokes our interest and attraction or, on the contrary, indifference or aversion when we contemplate a man-made work.

If you'd like to learn more about the Golden Ratio, you'll quickly discover that some authors make it an absolute and universal rule, while others, on the contrary, cry mystical fraud. It's up to you to make up your own mind.

What is certain is that the Golden Ratio is a mathematical and geometrical reality (middle-school students who have to solve equations like x2 - x - 1 = 0 won't disagree!).

Its presence in the structure of the human body may be debatable in its accuracy, but human proportions have indeed given rise to an organized and geometrically perfect system of measurement.

Since the advent of the decimal metric system, which no longer has anything to do with the human body, our vision of the relationship between the harmony that emanates from an object, a work of architecture or a work of art and the harmony of the proportions of the human body has been blurred. But the reflexes accumulated over the centuries die hard!