In search of the Golden Rectangle

In geometry, a Golden Rectangle is a rectangle whose ratio of width to height equals a number called the Golden Number, whose approximate value is 1.618. The Greek letter 𝚽 (pronounced "Fee") symbolizes this number.

This rectangle symbolizes the perfect harmony between two unequal lengths: its width and height.

This very special relationship between two lengths can be seen in the human body, for example, by comparing the size of the phalanges of our fingers, but also those of our hand and forearm, or the position of our navel in relation to the height of our body.

In search of the Golden Rectangle, we're going back in time to learn how people have measured and constructed their environment since ancient times.

We'll travel to ancient Egypt, the land of the Pharaohs, meet medieval cathedral builders, mathematicians and scientists such as Leonardo Fibonacci, Luca Pacioli and Leonardo da Vinci, architects and Italian Renaissance masters such as Andrea Palladio and Sandro Botticelli, philosophers of the 19th and early 20th centuries, and finally the famous Franco-Swiss architect Le Corbusier, who wanted to reconcile the system of measurements used by mankind for centuries with the metric system, which was born "only" in the wake of the French Revolution of 1789.

Through all these discoveries, we'll analyze the structure of several paintings by famous ancient painters such as Botticelli, Velasquez and Canaletto, as well as more contemporary ones like Van Gogh and Ferdinand Hodler, and understand why their works seem so harmonious.

After studying these paintings, we'll try to answer a tricky question: why do we find a work (architectural, pictorial) or object (craft or industrial) pleasing to the eye?

Why is it that we find a human creation harmonious ?

We'll then see that the proportions of this particular rectangle are very present in our environment.

Once you've finished reading this booklet, you'll have learned to recognize it, you'll know its history and you'll be able to recognize it (almost) everywhere !

The Egypt of the pharaohs

Today, we measure lengths in meters and centimeters, but this system of measurement, the decimal metric system, is a very recent development in human history.

In ancient Egypt, the standard measure was the cubit. The cubit is the distance between the tip of the elbow and the end of the outstretched hand.

Today, we call it the royal cubit or the great cubit. It measured between 52 and 54 centimetres today. Egyptian architects used this reference measurement in the construction of buildings and monuments.

Conquest after conquest, the territory of the Egyptian empire had become very extensive; the pharaohs decided to impose a single measure of the cubit to facilitate commercial transactions.

They had thousands of graduated rulers manufactured and distributed throughout the empire, so that everyone could use the same unit of measurement. The standard measure of the cubit was Pharaoh's own cubit. The ruler was subdivided into sub-measures of the cubit.

Egyptian builders used a rope with thirteen knots (twelve intervals) to trace the ground plans of their monuments and also to calculate angles. Each interval between two knots was equivalent to a cubit. The knotted rope could be used to draw many geometrical figures, including a right angle, as shown in the red figure opposite.

This triangle is known as a "3,4,5" or Egyptian triangle. It is still used today by some building tradesmen to ensure that an angle is straight.

The Roman Empire also used the cubit as a unit of measurement, as well as the foot, the palm and the finger. Over the centuries, and between different regions, the cubit measurement varied. In Roman times, it represented a length of around 45 cm.

The Middle Ages and cathedral builders

In the Middle Ages, cathedral builders used five measurements: the palm, the hand, the span, the foot and the cubit. The palm measures around 7.6 of our centimetres, the hand 12.4 cm, the span 20 cm, the foot 32.4 cm and the cubit 52.4 cm.

These measurements had a constant relationship to each other: the ratio of palm to hand was the same as that of foot to span, or cubit to foot. A skilled stonemason or carpenter was able to calculate each of these measures from a single one by geometric construction.

The architect in charge of a construction site carried a measuring stick with these five measurements, usually based on his own measurements. The rod was used as a reference for measurements throughout the entire project. But beware: these measurements varied from site to site, as the measurements of one architect could be different from those of another!

Apprenticeship in one of these building trades took a long time. The know-how was passed on to the apprentice by his masters. He then had to work on several building sites, and completed his apprenticeship by making a "masterpiece" which, after validation by his master craftsmen, enabled him to become a craftsman in his own right, and to know and use in particular those emblematic measures in his trade.

Companionship is still practiced today in a wide variety of fields, from stone and woodworking to catering and pastry-making.

The French Revolution and the birth of the metric system

Thumb, palm, palm, empan, foot and cubit were thus measurements directly inspired by the measurements of the human body.

But unlike the great eras of ancient Egypt and the Roman world, when mankind had succeeded in establishing a standard set of measurements over a large territory, the Middle Ages and royalty saw a multitude of different feet and cubits flourish: each region, and even each town, had its own official measurement, with the result that by the time of the French Revolution, there were no fewer than fifty different cubit measurements in the kingdom!

Indeed, if you measure the length of your own cubit and that of your neighbor's, you're bound to find different lengths!

The scientists of the revolution therefore wanted to establish a new system of measurement based on a standard that would make everyone agree, and developed what is known today as the decimal metric system.

The new metre was calculated as the ten-millionth part of a quarter of the earth's meridian. This new measurement system had nothing to do with human measurements.

In 1792, two scientists, Delambre and Méchain, were commissioned by King Louis XVI to measure the distance between Dunquerke and Barcelona by triangulation, in order to evaluate the length of the quarter of the terrestrial meridian. It took them more than seven years to complete the task.

We know today, thanks to the modern measuring instruments at our disposal, that the result achieved by Delambre and Méchain, with the means available at the time, was incredibly accurate.

Between 1796 and 1797, sixteen standard meters were placed in the busiest places in Paris to promote the new metric system.

In 1960, the definition of the metre was based on a wavelength: 1,650,763.73 times the wavelength, in vacuum, of orange radiation from the krypton 86 atom. In 1983, following major work on the speed of light and atomic clocks, the metre was redefined in terms of the speed of light, as equal to "the length of the path travelled by light in vacuum for 1/299,792,458 of a second". That's how abstract this definition has become, and how far removed it is from human measurements!

Although the metric system is the most widely used measurement system in the world today, human habits die hard: who hasn't measured the dimensions of a room in steps, or the length of a piece of furniture with the width of their outstretched hand (the span)? Intuitively, we still measure with our own bodies!

Today, the only countries not to use the metric system are the United States of America, Liberia and Burma. They still use what is known as the "imperial system of units". The system, established in 1824, was intended for use throughout the British Empire. It is still used in industries such as aeronautics and multimedia. (A computer or TV screen is measured in inches!)

The Golden Rectangle

Let's return to our Golden Rectangle: what could possibly be the relationship between the thirteen-knot rope (the Egyptian triangle), the foot and the cubit? Look closely at the figure below:

The relationship between side "5" and side "3" of the Egyptian triangle is the same as that between the cubit and the foot!

The same applies to the foot and the span, the span and the hand, and the hand and the palm.

This ratio, i.e. the division of the longest length by the shortest, was named the "Golden Number" at the beginning of the 20th century.

A Golden Rectangle is therefore a rectangle whose length to height ratio represents the Golden Number, i.e. 1.618.

The diagram below shows the steps involved in constructing a Golden Rectangle: it is obtained from a square ABCD. An arc of a circle with center I (middle of AB) and radius IC, intersects line AB at point E.
The rectangle AEFD is a golden rectangle. Indeed, the ratio of its width to its height is equal to 1.618, the value of the golden ratio.

AE/EF = (1 √5)/2 = 1.618

The new rectangle created BEFC is also a Golden rectangle, or EF/BE = 1.618

We'll see later that, without necessarily knowing it, we're surrounded by Golden Rectangles! Let's discover them together.

The Gustav Fechner experiment

Gustav Fechner (1801-1887) was a German philosopher and psychologist, known as one of the founders of experimental psychology.

He asked his students to choose the most harmonious of ten rectangles. Seven out of ten students chose the rectangle whose proportions corresponded to the Golden Rectangle!

Had Gustav Fechner's students intuitively recognized the proportions of the human body in the chosen rectangle? At least, that's what the psychologist wanted to prove with this experiment.

The first definition of the Golden Ratio

The Golden Ratio hasn't always been called that, but it has been known to mankind under other names for hundreds, if not thousands, of years.

Euclid, an ancient Greek mathematician (circa 300 BC), defined the division of a straight line segment into "extreme and middle reason" (i.e. into two unequal segments) when the ratio between the total length and the larger segment is equal to the ratio between the larger and the smaller segment. In his opinion, this is the most harmonious way of dividing a line segment into two unequal parts.

We saw above that cathedral builders knew the constant relationship between the palm, the palm, the span, the foot and the cubit. This relationship was a kind of trade secret. Only the initiated knew how to use it.

The Fibonacci sequence

In 1202, the mathematician Leonardo Fibonacci, also known as Leonardo of Pisa, published a book in which he described his discovery of an algebraic sequence that today bears his name, the "Fibonacci sequence". In his day, Leonardo Fibonacci was credited with introducing Indo-Arabic numbering (1,2,3,4,5,6,7,8,9) and the zero, which did not exist in Roman numbering, to Europe.

Legend has it that Fibonacci discovered this mathematical sequence by examining the reproduction of pairs of rabbits; one pair of rabbits begets another pair, which in turn begets two pairs of rabbits, which in turn have several babies and so on.

Let's take a closer look at this numerical sequence: it's a sequence of integers in which each element is the sum of the two terms preceding it. The first of these terms is zero, and the next is 1.

The sequence is written as follows; 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 etc. Indeed, 144, taken at random from this sequence, is the sum of 55 and 89, just as 5 is the sum of 3 and 2.

If we now divide one of the terms in the sequence by the previous term, for example 144 by 89, we obtain .... 1.618 !!!

There's an obvious connection between the Fibonacci sequence and the 5 emblematic measurements deduced from the proportions of the human body, used in the construction of sacred buildings in the Middle Ages.

These measures were subdivided into lines, one line representing the length of a barley grain. The palm was worth 34 lines, the hand 55, the span 89, the foot 144 and the cubit 233! We find this sequence of numbers in the Fibonacci sequence! It would seem, however, that Fibonacci himself did not make this connection at the time, which may seem logical; only architects and journeymen used the system of measurements in force at the time, and Leonardo Fibonacci was not one of them !

The Divine Proportion

We had to wait until the 15th century to find an official trace of this very special proportion; in 1496, Leonardo da Vinci illustrated a book by a famous contemporary mathematician, Luca Pacioli. This book, which describes polyhedra (three-dimensional geometric shapes) and deals with proportion as applied to geometry, architecture and the arts, is called "Divine proportion". Luca Pacioli compares the proportions of these geometric figures to human, and therefore divine, proportions, hence the title of his work.

Finally, in the 19th century, the German philosopher and mathematician Adolf Zeising spoke of the "golden section" (Goldener Schnitt) when analyzing the structure of the human skeleton.

At the beginning of the 20th century, Matila Ghyka, a Romanian diplomat with a passion for aesthetics, took inspiration from Adolf Zeising's work and named this ratio the "Golden Ratio". His book "Le nombre d'Or" (The Golden Ratio) was a great success with many designers and philosophers.

The mathematical formula for this number is (1 √5)/2, an approximate value of 1.618. Mathematicians have given the Greek letter φ (pronounced "phi") as their symbol for the golden ratio, in memory of Phidias, the architect who decorated the famous Parthenon in Athens.

If we had to give a simple, pictorial definition of the Golden Ratio, it would be the result of dividing the length of a cubit by the length of a foot, or the length of a forearm by the length of a hand. This ratio is found in many parts of the human body, and also in many geometric figures, such as the five-pointed star or the figures of Euclidean geometry.

In the figure below, you can see that the relationship between the cubit and the foot is identical to the relationship between the segments AC and AB, and the segments AB and BC of the five-pointed star.

So it's hardly surprising that this number, used by religious figures, architects and scientists of the time, has become such a myth. Note also the symbolic importance of the 5-pointed star in most religions, and the fact that we find it in many national flags.

The Golden Number and the human body

Try this experiment: you know how tall you are. Divide your height by this famous Golden Ratio, and measure the result of this division from the ground... you've found the height of your navel !

Now measure the length from the tip of your elbow to the end of your outstretched hand. Divide the result by 1.618 to obtain the length from the tip of your elbow to the wrist joint.

If you consider the three phalanges of your middle finger and the metacarpus, the bone that extends your phalanges to your wrist, the progression of their size is identical to that of the five measures used by cathedral builders! (Palm, hand, span, foot and cubit)

But we all have different measurements, and the proportion of one person's limbs is not strictly equal, to the nearest millimetre, to the proportion of another person's limbs!

If you take the measurements of your foot and cubit, and divide the length of your cubit by the length of your foot, you won't necessarily get 1.618, but something close.

The system devised by fellow cathedral builders was a geometric system inspired by the measurements of the human body. It represented a local standard, or construction norm, so that two stonemasons could cut two perfectly identical blocks of stone on a given day or two years later. Imagine the opposite, where each stonemason could cut a block of stone the size of his own cubit! All the blocks would be different, and building the monument would become impossible !

Le Corbusier and the Modulor

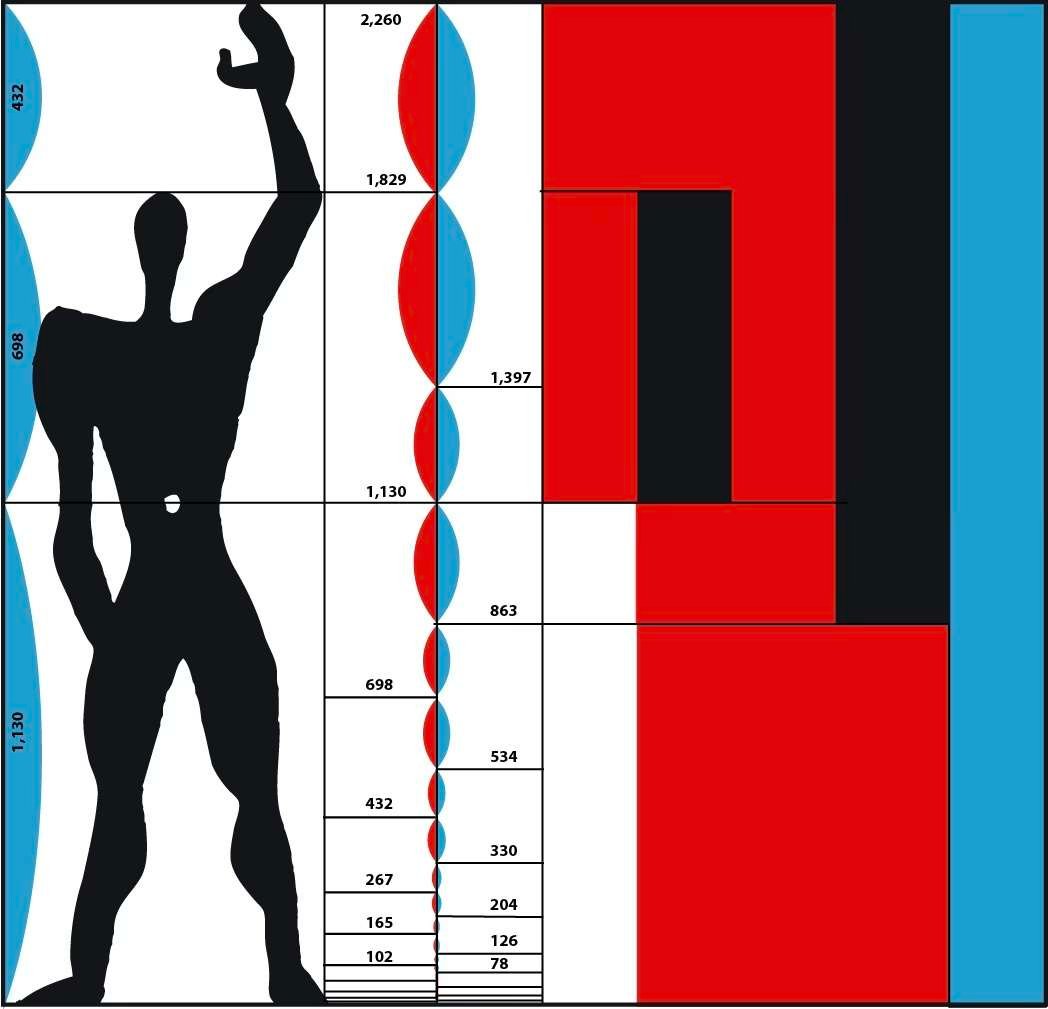
Closer to our own time, after the Second World War, the Franco-Swiss architect Charles-Édouard Jeanneret-Gris, known as "Le Corbusier", used this proportional system to structure the buildings he built, both in their interior and exterior proportions, wanting to ensure that their inhabitants could live in harmonious volumes corresponding to human proportions.

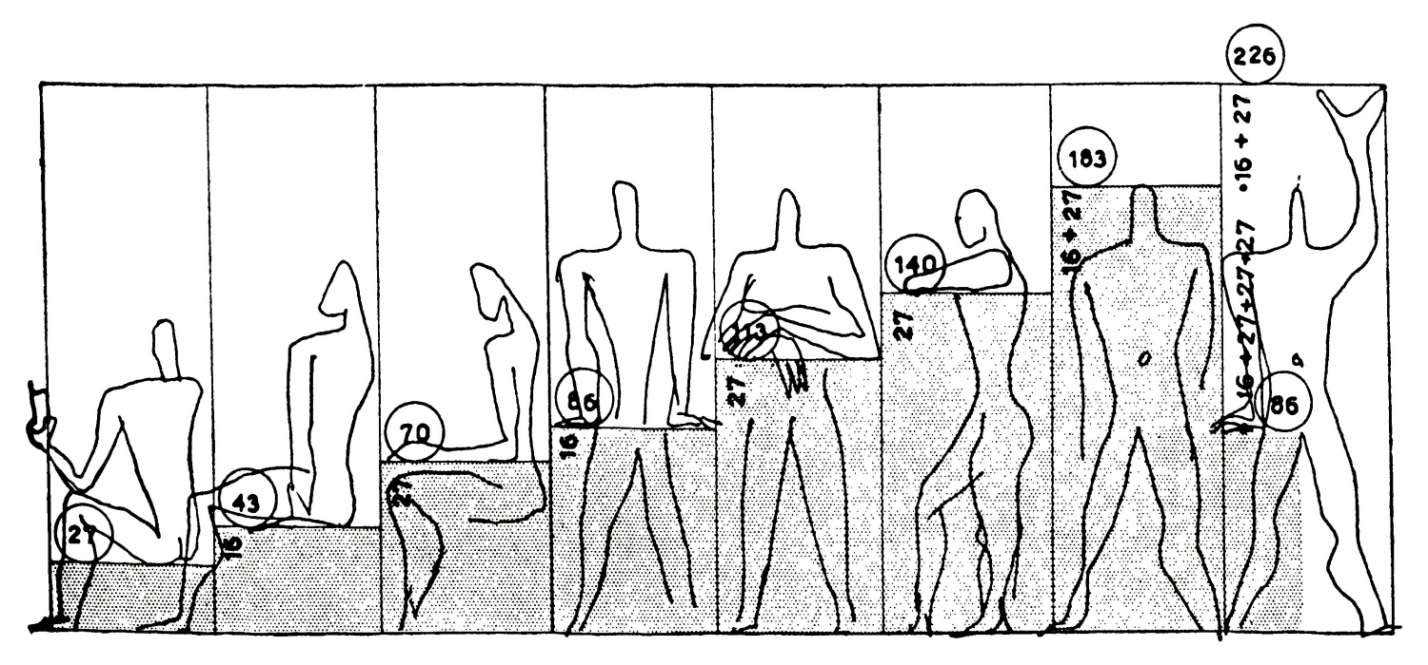
He gave it a name: the Modulor. Based on the proportions of the human body, the Modulor was a standardization tool that would enable all trades, from architect to carpenter, to quickly design volumes, doors and furniture with harmonious, human proportions.

The architect's sketch below defines the relationship between furniture size and the different postures of the human body.

Since the beginning of the 20th century, painters have also deliberately used this technique to structure their works, even if the external dimensions of their pictures were not those of a golden rectangle. The focal points and lines of force of their paintings were very often placed in positions calculated on this principle.

These proportions are widely used today by art photographers, architects, sculptors, craftsmen and designers.

Regulating lines

The term "regulating line" refers to the geometrical structure that serves as the basis for a drawing to balance it out. This drawing may be for a building, a sculpture, a garden or a painting.

As the architect Le Corbusier put it: "The regulating line doesn't bring poetic or lyrical ideas; it doesn't inspire the theme; it's not creative; it's a balancer. A problem of pure plasticity".

If we look more closely at the way these squares and concentric circles are distributed, we see that the relationships between these different geometric figures correspond proportionally to the relationships between palm, handbreath, span, foot and cubit.

The building's ground plan and facade therefore feature proportions that we find in the human body, and this is undoubtedly why we unconsciously find it harmonious.

The regulating line used by the architect is not the drawing of the building; it serves to proportion it and thereby give it a particular meaning and scope.

While regulating lines have certainly been used in architecture since antiquity, their use in painting dates back to the time when painters were able to understand and master perspective, i.e. to the early Renaissance.

Regulating lines have been and still are used in many fields: below, a line used in typography, dating back to the 13th century, regulating the position of text in relation to the size of the page. This type of layout is still used in computer graphics.

The figure on the left shows an analysis of the façade of the Duomo, Milan's cathedral, using a regular layout based on concentric circles and triangles.

The ground plan shows the proportions of a golden rectangle and the symbol of the cross, at the center of which stands the Duomo's spire.

When you analyze the ground plan and the facade of Reims Cathedral, shown below in the middle, it's hard to imagine that the architect didn't draw inspiration from hidden geometric figures and religious symbols when designing and building this edifice.

He certainly used a regulatory layout.

Note in passing that we find the famous Golden Rectangle in the dimensions of the facades of both religious buildings. And this rectangle is all the more familiar as it reminds us of the proportions of the human face.