Análisis de una obra de arte

El número áureo y la pintura

Antes hemos visto que las proporciones humanas fueron el origen de un sistema de medidas utilizado desde la antigüedad. La relación entre estas medidas se ha denominado Proporción Áurea, y encontramos huellas de ella en campos tan variados como las matemáticas, la geometría, la arquitectura y la tipografía.

Lo mismo ocurre en la pintura; desde el momento en que los pintores dominan la perspectiva y la representación pictórica se hace más realista, los pintores estructuran sus obras utilizando el sistema de medidas de su época.

En la Edad Media, la pintura era ante todo simbólica. El tamaño de las figuras estaba en función de su importancia y dignidad. La imagen de al lado es un ejemplo de perspectiva invertida, en la que los personajes menos importantes son más pequeños que los sujetos principales, aunque estén en primer plano.

A partir del Renacimiento, una perspectiva más realista comenzó a aparecer en las pinturas de los maestros de la época. La representación de la Anunciación de Fra Angelico (1400 - 1455) muestra que se habían adquirido los principios de la perspectiva y que las figuras tenían un tamaño realista en relación con los edificios.

En las décadas siguientes, los pintores utilizaron el sistema de medidas existente para estructurar sus obras: las figuras se situaban en lugares precisos, que hoy llamamos centros de interés o puntos focales.

Paul Veronese pintó las Bodas de Caná hacia 1562. La perspectiva está perfectamente dominada. Los grupos de personajes están cuidadosamente dispuestos, y vemos una verdadera puesta en escena cinematográfica, encuadrada según principios geométricos muy estrictos; la cuadrícula superpuesta al cuadro de Veronese que aparece a continuación nos permite imaginar esta puesta en escena de base geométrica.

El dominio general de estos efectos de representación permitía también al pintor "ver en grande". El tamaño de las obras de este periodo no tiene nada que ver con las iluminaciones de la Edad Media: ¡el cuadro mide casi 7 metros por 10!

Análisis de la estructura de un cuadro del Renacimiento italiano

Ahora sabemos lo suficiente sobre el sistema de medidas que precedió al sistema métrico decimal como para analizar la estructura de uno de los cuadros más famosos del Renacimiento italiano, el "Nacimiento de Venus", pintado por Sandro Botticelli hacia 1485.

El nacimiento de Venus

Venus nace de una concha. A su izquierda están Céfiro y Cloris. Céfiro es hijo de Eolo, dios de los vientos, y Cloris, su esposa, es una ninfa que reina sobre el imperio de las flores. Soplan sobre Venus como para desnudarla o secarla del agua en la que nació, pero también para purificarla y cubrirla de flores. A la derecha de Venus hay una "hora", hija de Zeus, una de las dueñas del tiempo. Parece querer cubrir a Venus con un paño adornado de flores para ocultar su desnudez, o para calentarla.

Botticelli se inspiró para su representación de Venus en Simonetta Cattaneo, una de las mujeres más bellas de Florencia, esposa del rico mercader Marco Vespucci y posiblemente amante de Giuliano de Médicis, cuyo hermano Lorenzo gobernaba la ciudad en aquella época. Simonetta murió muy joven, y el pintor la utilizó como modelo póstuma en muchos de sus cuadros. Amante platónico de la bella mujer, Botticelli quiso ser enterrado junto a ella cuando muriera. Los cuerpos de ambos reposan en Florencia, en la iglesia de Ognissanti.

Análisis de la posición de las figuras en el cuadro

Fíjate en la posición de las figuras en el cuadro. Fíjate también en la línea del horizonte, el límite entre el mar y el cielo. No está en el centro de la altura del cuadro, al igual que Venus, la figura central de la obra, no está exactamente en el centro del cuadro.

El cuadro mide 2,78 metros de ancho por 1,72 metros de alto. Estas medidas pueden parecer abstractas, pero no olvidemos que en aquella época se medía en pies y en codos.

Hoy sabemos que el codo medía entre 53 y 55 cm y el pie entre 33 y 36 cm. También sabemos que los pintores dividían la altura de su lienzo en ochos para cuadrarlo y colocar después los elementos principales de sus cuadros.

Si dividimos la altura de este cuadro entre 8, obtenemos 21,5 cm. Y si dividimos su anchura por 8, obtenemos 34,7 cm.

21.5 cm parece ser la medida de un palmo y 34,7 cm la de un pie, las medidas utilizadas en la época. ¿Tal vez fueran las medidas del propio Sandro Botticelli?

En aquella época, el cuadro debía de medir 5 x 3 codos, es decir, 8 x 5 pies, ¡o 13 x 8 imperios!

Cuadrar el cuadro con las medidas de la época

Empecemos a cuadrar el cuadro con una cuadrícula regular de cuadrados que midan, a la escala del cuadro, 35 cm de lado, es decir, la longitud de un pie. Podemos ver que los diferentes personajes del cuadro se distribuyen de la siguiente manera:

Céfiro y Cloris ocupan un rectángulo de 3 cuadrados de ancho por 5 de alto a la izquierda del cuadro, y Hora, hija de Zeus, el mismo rectángulo a su derecha.

Venus, por su parte, cabe en un rectángulo en el centro del cuadro, de 2 cuadrados de ancho por 5 de alto. La línea del horizonte parece coincidir con una de las líneas de la cuadrícula, y la concha que da a luz a Venus cabe en un rectángulo que tiene prácticamente 3 cuadrados de ancho por 2 de alto.

Recordarás que antes hemos dividido la anchura del cuadro por 8; ahora vamos a cuadrarlo con una cuadrícula regular de 21,5 cm cuadrados, dividiendo su altura por 8.

21,5 cm es la longitud aproximada del vano.

Céfiro y Cloris ocupan un rectángulo de 5 casillas de ancho por 8 de alto a la izquierda del cuadro, y Hora, hija de Zeus, el mismo rectángulo a su derecha.

Venus cabe en un rectángulo en el centro del cuadro, de 3 cuadrados de ancho por 8 de alto. Además, parece estar centrada en una de las líneas de esta nueva cuadrícula. La línea del horizonte coincide con una de las líneas de esta cuadrícula, y la concha está contenida en un rectángulo de 6 cuadrados de ancho por 3 de alto.

Podemos ver que la disposición del cuadro (línea del horizonte, posición de los distintos personajes) es prácticamente idéntica, tanto si el cuadro está dividido en 5x8 como en 8x13 cuadrados. La división de 8x13 parece más "refinada".

¡Obsérvese también que 3, 5, 8 y 13 figuran entre los primeros números de la famosa sucesión de Fibonacci, y que dividiendo 8 por 5, y 13 por 8, se obtiene un valor cada vez más próximo a 1.618!

Un trazado regulador basado en la proporción áurea

Si utilizáramos las herramientas actuales (calculadoras, ordenadores) para trazar una recta reguladora basada en la proporción áurea, procederíamos del siguiente modo: tomamos un rectángulo del mismo formato que el del cuadro de Botticelli y dividimos su anchura por 1,618: obtenemos la figura siguiente. La anchura total del rectángulo dividida por 1,618 nos permite trazar una línea vertical que divide el rectángulo en un cuadrado a la izquierda y un rectángulo a la derecha. Sigamos dividiendo el rectángulo pequeño de la misma manera dos veces.

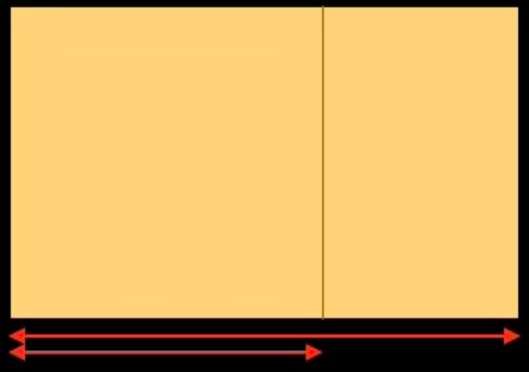
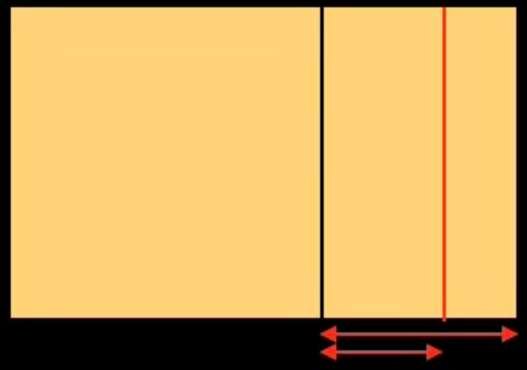
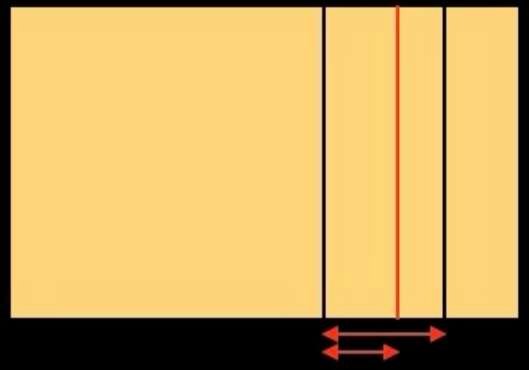
Hemos obtenido tres subdivisiones en el lado derecho del rectángulo inicial. Realicemos la misma operación en el lado izquierdo: obtenemos la figura de abajo a la izquierda. Hemos dividido el rectángulo inicial verticalmente 6 veces. Ahora lo dividiremos horizontalmente. Obtenemos la figura de abajo a la derecha.

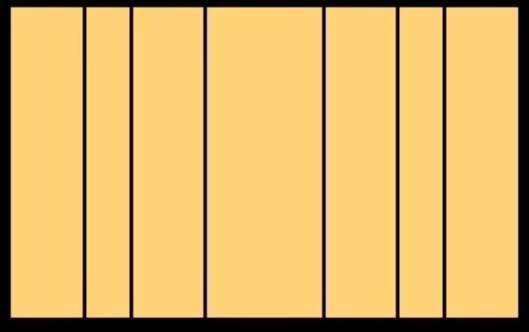
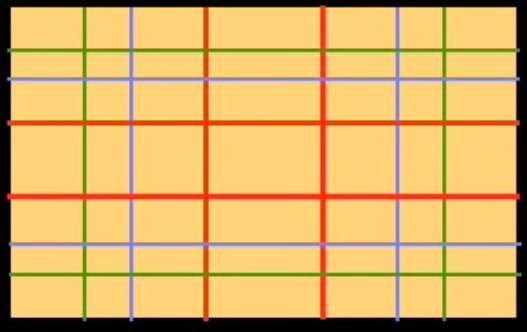
Las líneas rojas representan la primera división de la anchura y la altura del rectángulo inicial por la proporción áurea. La llamaremos división primaria.

Las líneas azules representan una división secundaria (es decir, la división de los rectángulos creados por la primera división), y las líneas verdes representan una división terciaria, es decir, la división de los rectángulos creados por la segunda división.

Ahora vamos a superponer este "gráfico regulador" moderno al cuadro de Botticelli, y a compararlo con los gráficos obtenidos utilizando las dos cuadrículas anteriores de 5x8 y 8x13.

Cuadrícula de 5x8

(Medida en pies)

Rejilla 8x13

(Medida en empans)

Trazado regular obtenido por el Golden Divider for Arts

Vemos que la división interna del cuadro es prácticamente idéntica: la línea del horizonte está más o menos en el mismo lugar, y las figuras y grupos de figuras del cuadro ocupan las mismas zonas.

¿Qué podemos deducir de ello?

Sabemos que Botticelli no disponía entonces ni de calculadora ni de "cinta métrica". Así que sólo podía colocar los puntos focales de su cuadro utilizando sus propias medidas.

Botticelli había aprendido su arte de un pintor-monje llamado Fra Filippo Lippi, que sin duda le había enseñado a estructurar un cuadro simbólicamente, es decir, utilizando medidas y proporciones humanas y, por tanto, divinas. Este saber hacer era un secreto de oficio, como el de los maestros de obras, y se transmitía de maestro a alumno, de generación en generación.

En cuanto a la línea reguladora de la pintura de Botticelli, no es en absoluto seguro que el pintor conociera la secuencia de Fibonacci, ni siquiera que conociera la proporción áurea. ¡No podemos imaginarnos a Sandro Botticelli sacando una calculadora -que no existía en aquella época- y dividiendo la altura y la anchura de su cuadro por (1 √5)/2!

Pero ahora sabemos que dividiendo la altura de su lienzo por 8, y utilizando las medidas de su época, el resultado era prácticamente el mismo. Este secreto de fabricación, sin duda de inspiración religiosa, era por tanto accesible a través de la simple geometría: basta una cuerda para dividir una longitud en 2, luego en 4 y en 8. Del mismo modo, quien utiliza una cuerda de 13 nudos para comprobar un ángulo recto no tiene ni idea del significado histórico, geométrico y casi místico de la herramienta que maneja.

La noción del número áureo era inherente al sistema de medidas utilizado por nuestros antepasados: lo utilizaban sin necesidad de conocerlo. De hecho, la combinación de medidas utilizadas, como el codo, el pie y el empan, hacía que las proporciones "áureas" aparecieran "matemáticamente".

Inconscientemente encontramos proporciones familiares y humanas en la pintura de Botticelli, y sin duda por eso la obra nos parece equilibrada.

Compare la colocación de la línea del horizonte en relación con la altura del cuadro y la posición de la articulación de la muñeca en un antebrazo humano. Los diferentes grupos que componen el cuadro también están dispuestos según la misma lógica.

Según el sistema de medidas utilizado por los constructores de catedrales, si la longitud del codo es la distancia desde el codo hasta el extremo de la mano extendida, entonces la longitud del pie sería la del antebrazo sin la longitud de la mano, y la longitud de la mano equivaldría a la del palmo, es decir, la anchura de la mano con los dedos extendidos.

Análisis de la estructura de cuadros de distintas épocas

Diego Velasquez - Venus con espejo - 1647

Fíjate en la disposición del cuerpo de Venus, que encaja en un rectángulo alargado que ocupa dos tercios de la parte inferior del cuadro (línea de puntos arriba). Su busto encaja en un rectángulo, marcado aquí en rojo, en la esquina inferior derecha del cuadro. Un rectángulo idéntico enmarca al querubín, arriba a la izquierda, en simetría diagonal.

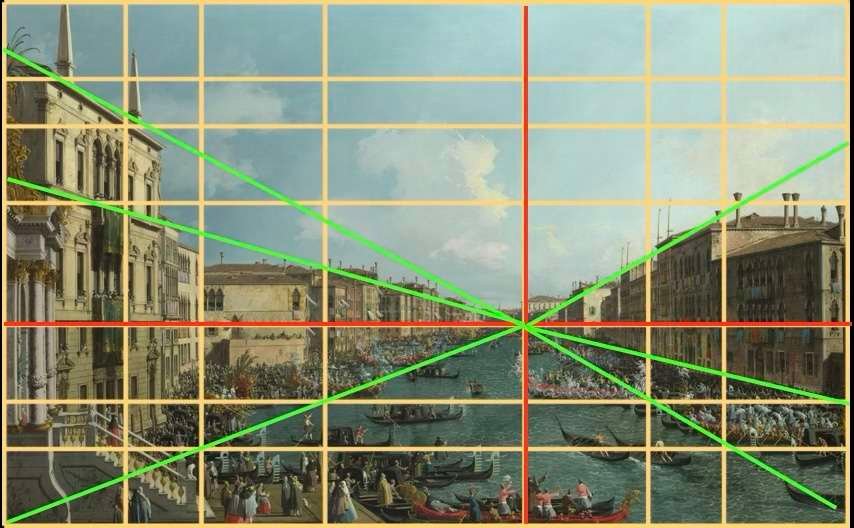
Canaletto - Regata en el Gran Canal - 1740

Obsérvese aquí la colocación de la línea del horizonte, y el punto de fuga del cuadro situado sobre ella, en la intersección de las dos líneas rojas. Todas las líneas de fuga, en verde, convergen en este único punto de fuga.

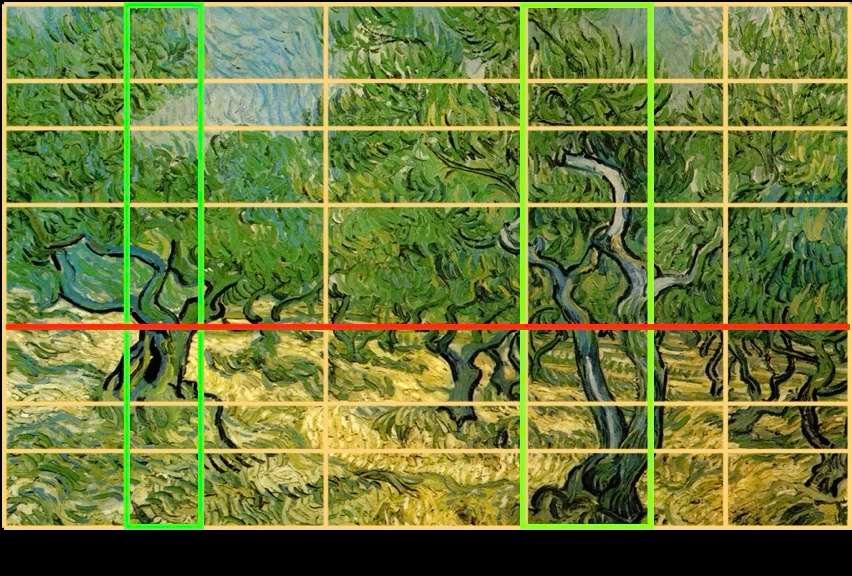
Vincent Van Gogh - Los olivos - hacia 1889

La línea del horizonte, aquí en rojo, marca el límite entre el suelo y el follaje de los olivos. Los dos troncos principales, en verde, se sitúan en el centro de dos rectángulos delimitados por las flechas situadas bajo el cuadro. Aunque cada árbol es simétrico en sí mismo, la asimetría de los dos árboles confiere al cuadro una dinámica armoniosa.

Ferdinand Hodler - El Delta del Maggia antes del amanecer - 1893

La "división" del cuadro se hace aquí evidente gracias a la cuadrícula estructural: el rectángulo alargado de la parte superior delimita la cordillera, el del centro el hielo y el de la parte inferior el agua clara. La línea del horizonte, en rojo, está delimitada por los dos rectángulos altos.

A continuación se muestran dos pinturas de maestros cuyas proporciones externas difieren de las del rectángulo áureo. Sin embargo, la estructura interna de estos cuadros sugiere que se utilizó la proporción áurea, de forma consciente o no.

Leonardo da Vinci - La Anunciación - 1472

Este cuadro no tiene el formato de un rectángulo áureo, pero la división interna de su estructura, en rojo, establecida según la regla de oro, revela cuatro rectángulos cuyas líneas delimitan la línea del horizonte, el ángulo del edificio y la posición respectiva de las figuras.

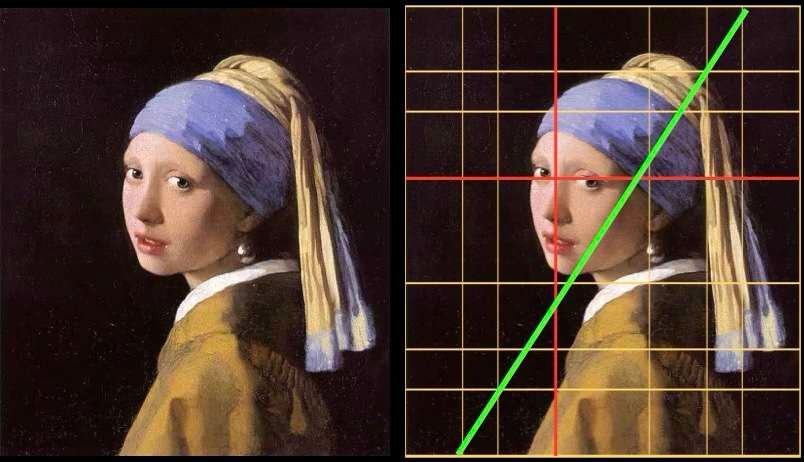
Johannes Vermeer - La joven de la perla - 1665

Una mirada rápida al cuadro sugiere que el rostro de la joven está en el centro. Pero si superponemos una cuadrícula estructural basada en la proporción áurea, vemos la posición específica del rostro de la joven: las líneas rojas determinan con precisión la alineación de sus ojos y el eje vertical de su cara. Una línea diagonal, de color verde en la imagen, delimita la luz y la sombra.

El número áureo y el diseño industrial

No cabe duda de que existe una relación entre estética y funcionalidad: en otras palabras, lo que es bello es funcional, y todo lo que es funcional es bello, al igual que en el cuerpo humano. Los diversos ejemplos que se exponen a continuación ilustran la forma en que el Número de Oro nos señala su presencia a diario.
Muchos objetos de nuestra vida cotidiana tienen proporciones cercanas a las del rectángulo áureo y, por tanto, a las del cuerpo humano.

El formato de ciertos libros, una radio, una caja de perfume o la relación entre las dimensiones de una ventana son ejemplos sorprendentes. Observará que muchas ventanas tienen las proporciones del Rectángulo de Oro, y no es de extrañar que así sea; se adoptó la costumbre de dar a las ventanas comunes las siguientes dimensiones: tres pies de ancho por tres codos de alto, ¡las proporciones perfectas de un Rectángulo de Oro!

Abajo, un patrón regular se ha superpuesto a siluetas de barcos, aviones, coches e incluso pistolas. La asimetría aparente de los volúmenes se denomina simetría dinámica.

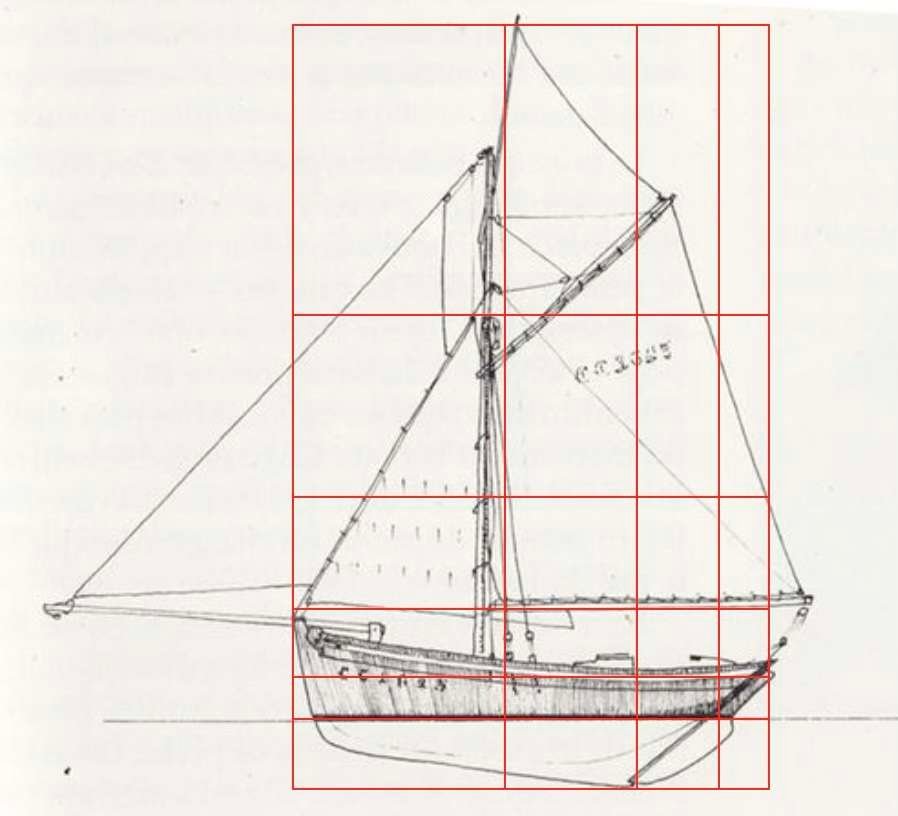
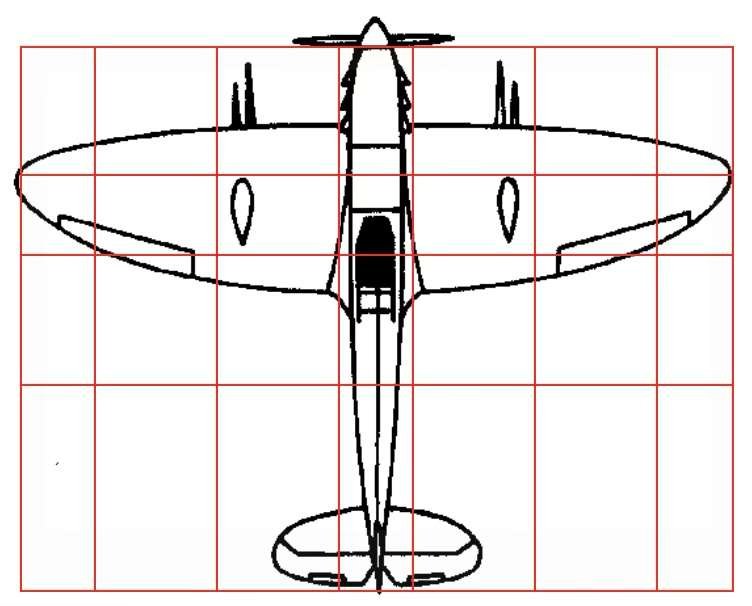
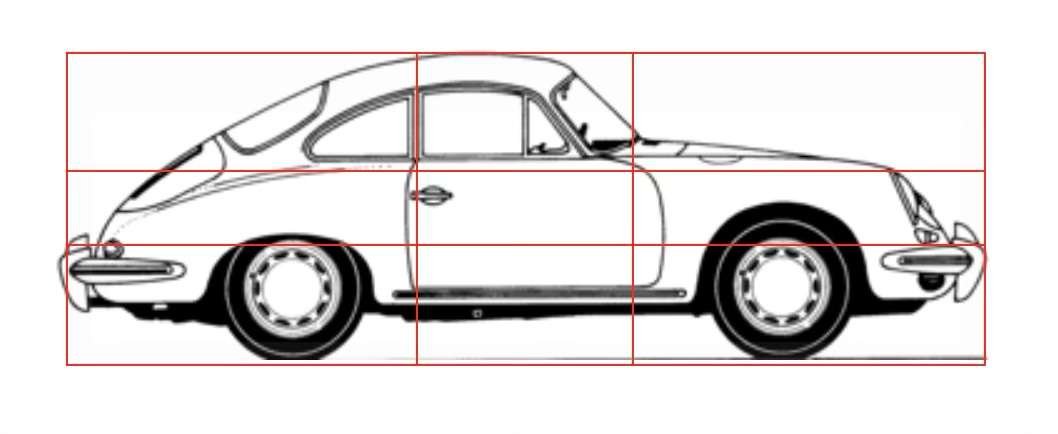
Las proporciones utilizadas en la construcción naval, aeronáutica, automovilística y militar demuestran que la estética y la funcionalidad están inextricablemente unidas.

El número áureo y la arquitectura

El número áureo inspiró la arquitectura de la Antigüedad, la Edad Media y el Renacimiento, gracias, como hemos visto, a un sistema de medidas basado en este concepto.

La pirámide de Jufu, el Partenón de Atenas, la catedral de Notre Dame de París, así como la mayoría de los edificios sagrados construidos en Europa en la Edad Media, la Gran Mezquita de Kairuán en Túnez y el Taj Mahal en la India son ejemplos reconocidos.

Pero, ¿se sigue utilizando hoy en día el número áureo en esta disciplina?

Tras la Segunda Guerra Mundial, el arquitecto franco-suizo Charles-Édouard Jeanneret-Gris, conocido como Le Corbusier (1887 - 1965), retomó las teorías del arquitecto romano Vitruvio, tratando de adaptar el urbanismo, la arquitectura e incluso el mobiliario a la morfología humana.

En 1945, desarrolló un concepto arquitectónico conocido como Modulor, que permitía estandarizar el entorno humano según sus propias proporciones.

El nombre "Modulor" es una contracción de "module" (módulo) y "nombre d'or" (nombre de oro).

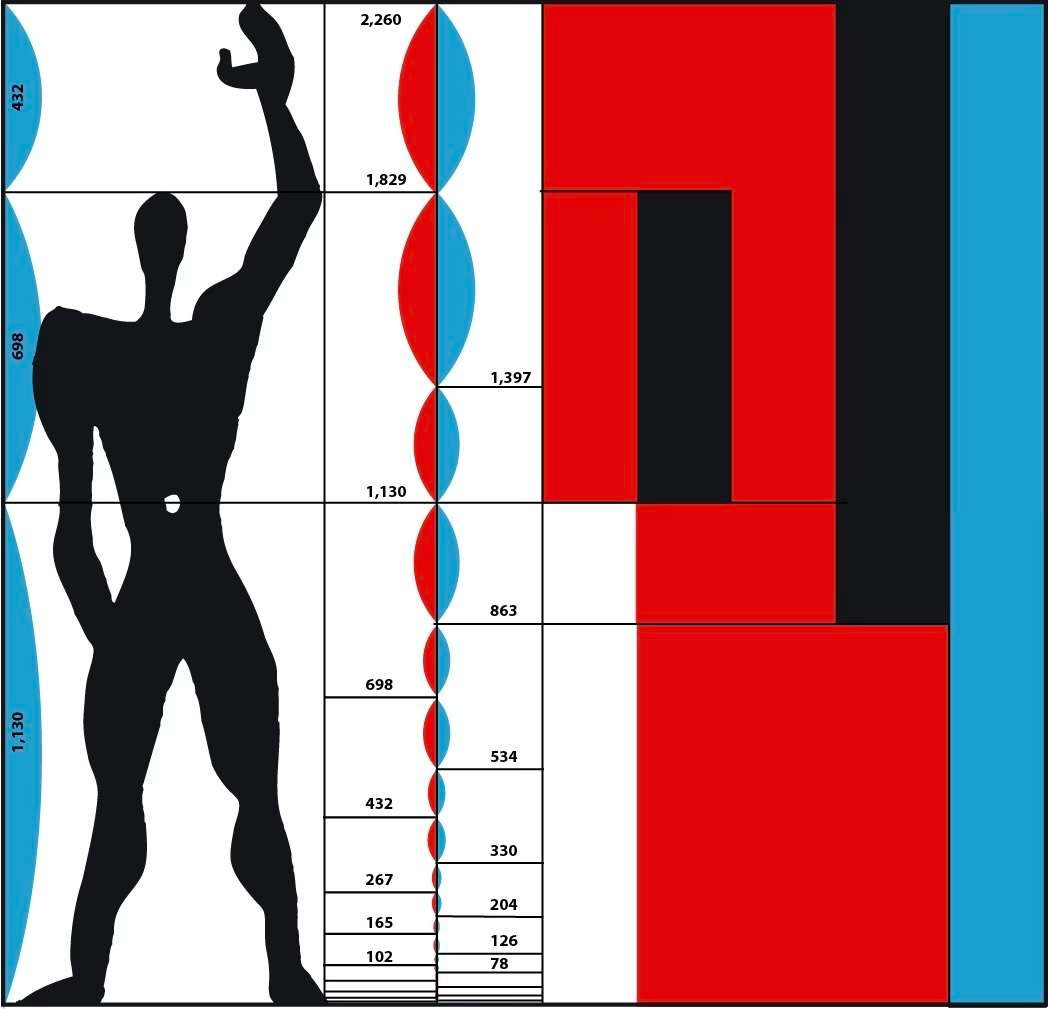
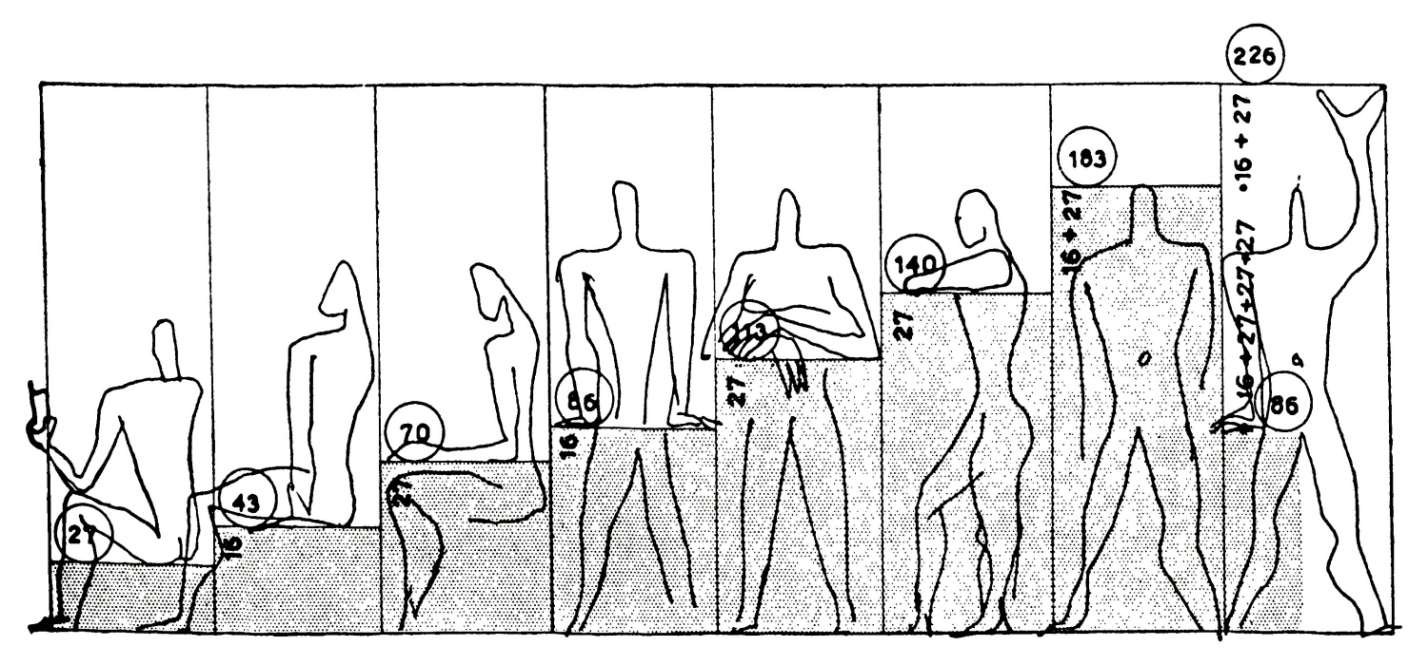
Aunque los proyectos de Le Corbusier son relativamente escasos, siendo los más conocidos el Museo Nacional de Arte Occidental de Tokio (1959), la ciudad de Chandigarh en la India (1951), La villa Savoye (1928-1931), la Cité Radieuse de Marsella (1952) y la capilla de Notre-Dame-du-Haut de Ronchamp (1953-1955), influyó sin embargo en toda una generación de arquitectos de todo el mundo.

La idea de diseñar viviendas y arquitectura interior compatibles con las proporciones humanas sigue atrayendo hoy en día a un gran número de arquitectos de todas las nacionalidades.

¿Hemos encontrado el Rectángulo de Oro?

Sí, porque estamos literalmente rodeados de él, si nos fijamos bien Por supuesto, ya no medimos lo que nos rodea en pies y codos, y el sistema métrico decimal, al ser tan abstracto y tan distinto del cuerpo humano, ha difuminado sin duda las líneas de nuestra forma de percibir y evaluar nuestro entorno.

Pero los hábitos adquiridos a lo largo de los siglos se han mantenido; la evaluación de una figura humana, una obra arquitectónica, un cuadro o incluso un objeto sigue implicando una comparación inconsciente con las proporciones humanas.

La proporción áurea, esa relación especial entre la altura y la anchura de un rectángulo de oro, se encuentra inconscientemente en una mano o un rostro, que se ajustan más o menos a esta figura geométrica.

Nuestra idea de la armonía y la belleza es inseparable de nuestra percepción del cuerpo humano. Es sin duda este análisis inconsciente que hacemos constantemente el que provoca nuestro interés y atracción o, por el contrario, nuestra indiferencia o aversión cuando contemplamos una obra hecha por el hombre.

Si quiere saber más sobre la Proporción Áurea, pronto descubrirá que algunos autores la convierten en una regla absoluta y universal, mientras que otros afirman que se trata de un truco místico. Usted decide.

Lo que sí es cierto es que la Proporción Áurea es una realidad matemática y geométrica (los alumnos de secundaria que tienen que resolver ecuaciones como x2 - x - 1 = 0 no estarán en desacuerdo).

Su presencia en la estructura del cuerpo humano puede ser discutible en cuanto a su exactitud, pero las proporciones humanas han dado lugar a un sistema de medidas organizado y geométricamente perfecto.

Desde la llegada del sistema métrico decimal, que ya no tiene nada que ver con el cuerpo humano, se ha difuminado nuestra visión de la relación entre la armonía que emana de un objeto, una obra de arquitectura o una obra de arte y la armonía de las proporciones del cuerpo humano. Pero los reflejos acumulados a lo largo de los siglos ¡mueren con fuerza!